Question

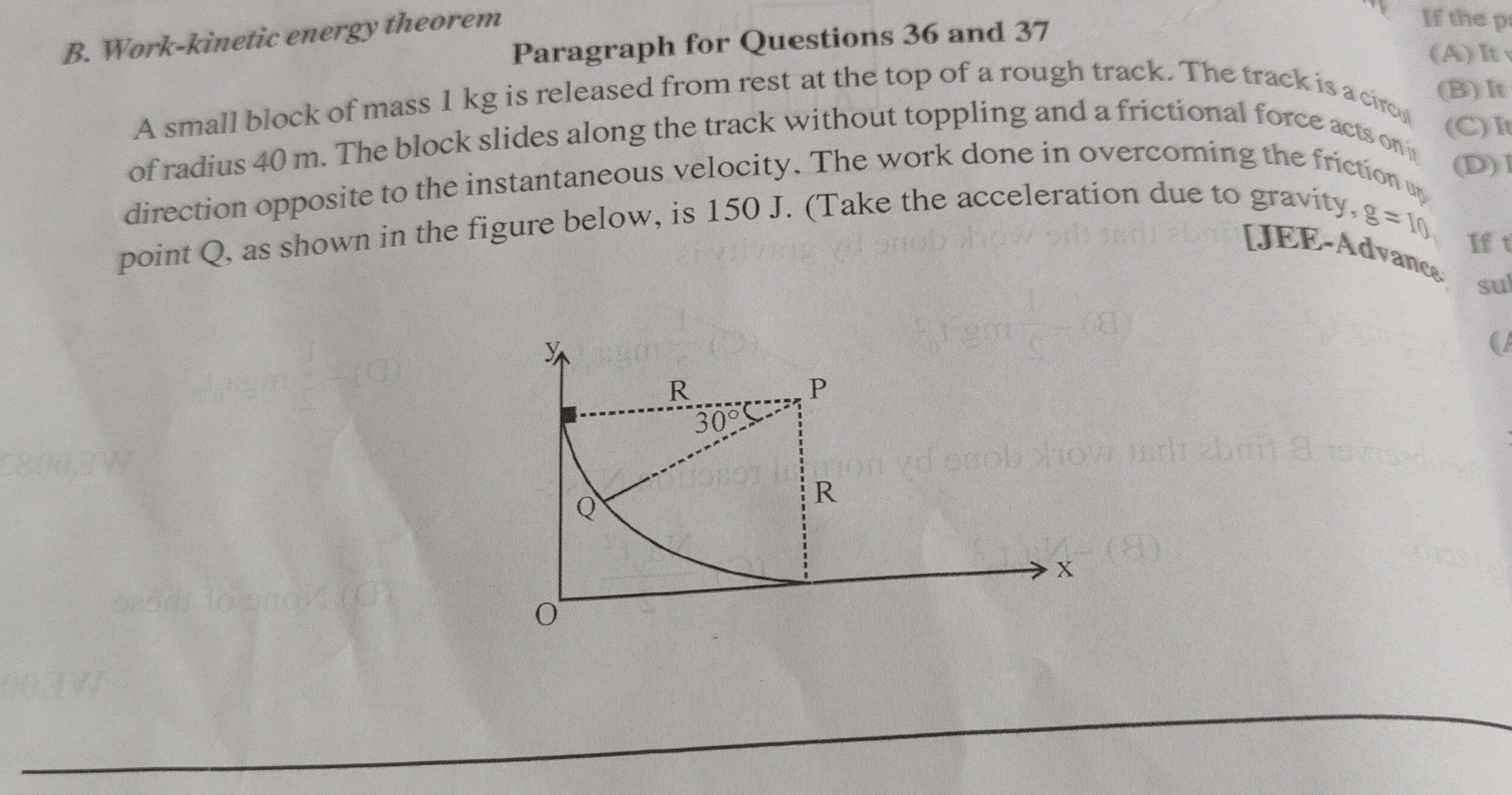
A small block of mass 1 kg is released from rest at the top of a rough track. The track is a circular of radius 40 m. The block slides along the track without toppling and a frictional force acts on it direction opposite to the instantaneous velocity. The work done in overcoming the friction up to point Q, as shown in the figure below, is 150 J. (Take the acceleration due to gravity, g = 10. [JEE-Advance.]

Answer 1

The question is descriptive and doesn't have a single correct answer.

Answer 2

The problem can be solved using the Work-Energy Theorem, which states that the net work done on an object is equal to the change in its kinetic energy. In the presence of non-conservative forces like friction, the principle of energy conservation can be stated as:

Initial Energy + Work done by non-conservative forces = Final Energy

$E_{initial} + W_{non-conservative} = E_{final}$

Where $E = KE + PE$.

Given:

• Mass of the block, $m = 1 \text{ kg}$

• Radius of the circular track, $R = 40 \text{ m}$

• Acceleration due to gravity, $g = 10 \text{ m/s}^2$

• Work done in overcoming friction, $W_{friction\_overcome} = 150 \text{ J}$. This means the work done by friction is $W_{friction} = -150 \text{ J}$.

Let's define the initial and final states:

• Initial state (P): The block is released from rest at the top of the track.

• Final state (Q): The block reaches point Q on the track.

1. Determine the initial and final heights:

   From the diagram, the origin O is at the bottom of the circular arc. The block starts at the top of the track, which is at a height $R$ from the horizontal x-axis. So, the initial height $h_P = R = 40 \text{ m}$.

   Point Q is on the circular arc. The diagram shows that the angle between the radius OQ and the horizontal x-axis is $30^\circ$.

   Therefore, the height of point Q from the x-axis is $h_Q = R \sin(30^\circ)$.

   $h_Q = 40 \times \frac{1}{2} = 20 \text{ m}$.

2. Calculate the initial and final potential and kinetic energies:

   • Initial state (P):

     Since the block is released from rest, its initial kinetic energy is $KE_P = 0$.

     Initial potential energy (relative to the x-axis) is $PE_P = mgh_P = 1 \times 10 \times 40 = 400 \text{ J}$.

   • Final state (Q):

     Let the speed of the block at Q be $v_Q$.

     Final kinetic energy is $KE_Q = \frac{1}{2}mv_Q^2 = \frac{1}{2} \times 1 \times v_Q^2 = \frac{1}{2}v_Q^2$.

     Final potential energy (relative to the x-axis) is $PE_Q = mgh_Q = 1 \times 10 \times 20 = 200 \text{ J}$.

3. Apply the Work-Energy Theorem:

   The work done by non-conservative forces (friction) is negative because it opposes the motion.

   $E_P + W_{friction} = E_Q$

   $KE_P + PE_P + W_{friction} = KE_Q + PE_Q$

   $0 + 400 \text{ J} + (-150 \text{ J}) = \frac{1}{2}v_Q^2 + 200 \text{ J}$

   $400 - 150 = \frac{1}{2}v_Q^2 + 200$

   $250 = \frac{1}{2}v_Q^2 + 200$

   $250 - 200 = \frac{1}{2}v_Q^2$

   $50 = \frac{1}{2}v_Q^2$

   $v_Q^2 = 100$

   $v_Q = \sqrt{100}$

   $v_Q = 10 \text{ m/s}$

The speed of the block when it reaches point Q is $10 \text{ m/s}$.