Question

Use simpson's $\frac{1}{3}$ rd rule to obtain $\int_{1}^{2}\frac{1}{x}dx$ dividing the interval into four parts.

Answer 1

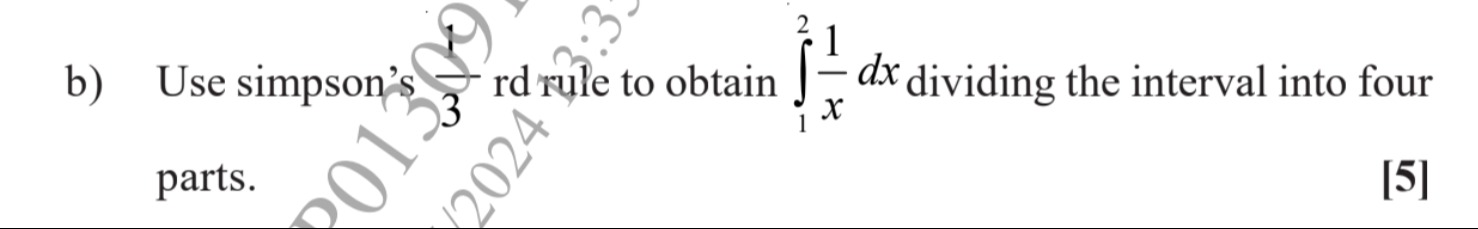
The approximate value of the integral is $\frac{1747}{2520}$.

Answer 2

To evaluate the definite integral $\int_{1}^{2}\frac{1}{x}dx$ using Simpson's $\frac{1}{3}$ rule with $n=4$ subintervals, we follow these steps:

1. Identify the parameters:
   The function is $f(x) = \frac{1}{x}$.
   The interval is $[a, b] = [1, 2]$.
   The number of subintervals is $n = 4$.

2. Calculate the width of each subinterval:
   $h = \frac{b-a}{n} = \frac{2-1}{4} = \frac{1}{4} = 0.25$.

3. Determine the points $x_i$:
   The points are $x_i = a + i \cdot h$ for $i = 0, 1, 2, 3, 4$.
   $x_0 = 1 + 0(0.25) = 1$
   $x_1 = 1 + 1(0.25) = 1.25$
   $x_2 = 1 + 2(0.25) = 1.50$
   $x_3 = 1 + 3(0.25) = 1.75$
   $x_4 = 1 + 4(0.25) = 2$

4. Evaluate the function $f(x) = \frac{1}{x}$ at these points:
   $f(x_0) = f(1) = \frac{1}{1} = 1$
   $f(x_1) = f(1.25) = \frac{1}{1.25} = \frac{1}{5/4} = \frac{4}{5}$
   $f(x_2) = f(1.50) = \frac{1}{1.50} = \frac{1}{3/2} = \frac{2}{3}$
   $f(x_3) = f(1.75) = \frac{1}{1.75} = \frac{1}{7/4} = \frac{4}{7}$
   $f(x_4) = f(2) = \frac{1}{2}$

5. Apply Simpson's $\frac{1}{3}$ rule:
   The formula for Simpson's $\frac{1}{3}$ rule with $n=4$ is:
   $\int_{a}^{b} f(x) dx \approx \frac{h}{3} [f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + f(x_4)]$

   Substitute the values:
   $\int_{1}^{2}\frac{1}{x}dx \approx \frac{0.25}{3} [f(1) + 4f(1.25) + 2f(1.50) + 4f(1.75) + f(2)]$
   $\int_{1}^{2}\frac{1}{x}dx \approx \frac{1/4}{3} [1 + 4(\frac{4}{5}) + 2(\frac{2}{3}) + 4(\frac{4}{7}) + \frac{1}{2}]$
   $\int_{1}^{2}\frac{1}{x}dx \approx \frac{1}{12} [1 + \frac{16}{5} + \frac{4}{3} + \frac{16}{7} + \frac{1}{2}]$

6. Calculate the sum inside the bracket:
   Sum $= 1 + \frac{16}{5} + \frac{4}{3} + \frac{16}{7} + \frac{1}{2}$
   Find the least common multiple (LCM) of the denominators (1, 5, 3, 7, 2), which is 210.
   Sum $= \frac{210}{210} + \frac{16 \times 42}{210} + \frac{4 \times 70}{210} + \frac{16 \times 30}{210} + \frac{1 \times 105}{210}$
   Sum $= \frac{210 + 672 + 280 + 480 + 105}{210} = \frac{1747}{210}$

7. Calculate the approximate integral value:
   $\int_{1}^{2}\frac{1}{x}dx \approx \frac{1}{12} \times \frac{1747}{210} = \frac{1747}{2520}$

   As a decimal, $\frac{1747}{2520} \approx 0.693253968...$

The integral $\int_{1}^{2}\frac{1}{x}dx$ is approximated using Simpson's $\frac{1}{3}$ rule. The interval $[1, 2]$ is divided into $n=4$ subintervals, each of width $h = \frac{2-1}{4} = 0.25$. The points $x_i$ are $1, 1.25, 1.5, 1.75, 2$. The function $f(x) = \frac{1}{x}$ is evaluated at these points. Simpson's $\frac{1}{3}$ rule formula $\frac{h}{3} [f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + f(x_4)]$ is applied using the calculated values $h=0.25$, $f(1)=1$, $f(1.25)=4/5$, $f(1.5)=2/3$, $f(1.75)=4/7$, and $f(2)=1/2$. The values are substituted into the formula, and the expression is calculated to obtain the approximate integral value.