Question
Question: Prove that the straight $\frac{x}{a}-\frac{by}{b}=m$ and $\frac{x}{a}+\frac{y}{b}=\frac{1}{m}$ alway...
Prove that the straight ax−bby=m and ax+by=m1 always meet on the hyperbola.
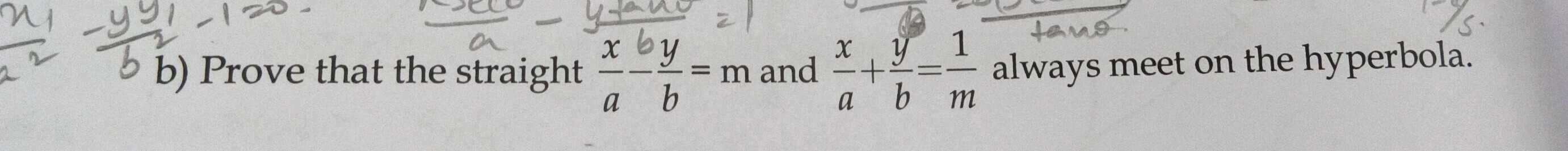
a2x2−b2y2=1
Solution
Let the two given straight lines be
(1) ax−bby=m
(2) ax+by=m1
Assuming b=0, the term bby simplifies to y. So, the first equation becomes:
(1) ax−y=m
Now we have the system of equations:
(1) ax−y=m
(2) ax+by=m1
Let the intersection point be (x,y). We solve this system for x and y.
Subtract equation (1) from equation (2):
(ax+by)−(ax−y)=m1−m
ax+by−ax+y=m1−m
by+y=m1−m2
y(1+b1)=m1−m2
y(bb+1)=m1−m2
y=m(b+1)b(1−m2)
Now substitute the expression for y back into equation (1) to find x:
ax=m+y
ax=m+m(b+1)b(1−m2)
ax=m(b+1)m2(b+1)+b(1−m2)
ax=m(b+1)m2b+m2+b−bm2
ax=m(b+1)m2+b
x=m(b+1)a(m2+b)
The coordinates of the intersection point are (x,y)=(m(b+1)a(m2+b),m(b+1)b(1−m2)).
We need to show that this point lies on a hyperbola. The phrase "always meet on the hyperbola" implies that the locus of the intersection point (x,y) as m varies is a hyperbola. We need to find the equation of this locus by eliminating m.
From the expressions for x and y, we can write:
ax=m(b+1)m2+b
by=m(b+1)1−m2
Let's try to manipulate these expressions to eliminate m.
Consider the sum and difference of ax and by:
ax+by=m(b+1)m2+b+m(b+1)1−m2=m(b+1)m2+b+1−m2=m(b+1)b+1=m1
This matches the second given equation, which is expected.
ax−by=m(b+1)m2+b−m(b+1)1−m2=m(b+1)m2+b−(1−m2)=m(b+1)m2+b−1+m2=m(b+1)2m2+b−1
This does not seem to directly lead to a simple hyperbola equation.
Let's reconsider the probable intended form of the question based on standard problems of this type. If the equations were ax−by=m and ax+by=m1, the solution would be much cleaner and lead to a standard hyperbola form. Let's assume there was a typo in the first equation and it should have been ax−by=m.
Assuming the lines are:
(1') ax−by=m
(2') ax+by=m1
Add (1') and (2'):
(ax−by)+(ax+by)=m+m1
a2x=m+m1
ax=21(m+m1)
Subtract (1') from (2'):
(ax+by)−(ax−by)=m1−m
b2y=m1−m
by=21(m1−m)
Now, square both expressions:
(ax)2=(21(m+m1))2=41(m2+2+m21)
(by)2=(21(m1−m))2=41(m21−2+m2)
Subtract the second squared expression from the first:
(ax)2−(by)2=41(m2+2+m21)−41(m2−2+m21)
=41[(m2+2+m21)−(m2−2+m21)]
=41[m2+2+m21−m2+2−m21]
=41[4]
=1
So, we get the equation a2x2−b2y2=1. This is the equation of a hyperbola. The intersection point (x,y) satisfies this equation regardless of the value of m. Thus, the intersection point always lies on the hyperbola a2x2−b2y2=1.
This result strongly suggests that the first equation in the question was intended to be ax−by=m. If we strictly follow the given equation ax−bby=m, which simplifies to ax−y=m, the resulting locus is not a standard hyperbola form A2x2±B2y2=1 or B2y2−A2x2=1. It is possible that the intended hyperbola is not centered at the origin or has a more complex form, but without further context or clarification, the most reasonable interpretation is that there was a typo in the first equation.
Assuming the intended question used the lines ax−by=m and ax+by=m1, the proof is as follows:
Let the equations of the lines be
L1: ax−by=m
L2: ax+by=m1
To find the intersection point (x,y), we solve the system of equations.
Adding L1 and L2 gives:
(ax−by)+(ax+by)=m+m1
a2x=m+m1
ax=21(m+m1)
Subtracting L1 from L2 gives:
(ax+by)−(ax−by)=m1−m
b2y=m1−m
by=21(m1−m)
To find the locus of the intersection point, we eliminate the parameter m. We square the expressions for ax and by:
(ax)2=41(m+m1)2=41(m2+2+m21)
(by)2=41(m1−m)2=41(m21−2+m2)
Subtracting the second squared equation from the first:
(ax)2−(by)2=41(m2+2+m21)−41(m2−2+m21)
a2x2−b2y2=41[(m2+2+m21)−(m2−2+m21)]
a2x2−b2y2=41[4]
a2x2−b2y2=1
This equation is the standard equation of a hyperbola. Since the coordinates (x,y) of the intersection point satisfy this equation for any value of m (where m=0), the intersection point always lies on this hyperbola.
