Question
Question: $\lim_{x\to\infty} \frac{2x^2+x-5}{4x^3+5x+1}$...
limx→∞4x3+5x+12x2+x−5
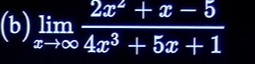
0
Solution
To evaluate the limit of a rational function as x approaches infinity, we can divide both the numerator and the denominator by the highest power of x present in the denominator.
The given limit is: limx→∞4x3+5x+12x2+x−5
The highest power of x in the denominator is x3. Divide every term in the numerator and the denominator by x3: limx→∞x34x3+x35x+x31x32x2+x3x−x35
Simplify the terms: limx→∞4+x25+x31x2+x21−x35
As x→∞, any term of the form xnc where c is a constant and n>0 approaches 0. Therefore, as x→∞: x2→0 x21→0 x35→0 x25→0 x31→0
Substitute these limiting values into the expression: 4+0+00+0−0=40=0
Alternatively, for a rational function Q(x)P(x), as x→∞: If the degree of the numerator is less than the degree of the denominator, the limit is 0. In this case, the degree of the numerator (2x2+x−5) is 2. The degree of the denominator (4x3+5x+1) is 3. Since 2<3, the limit is 0.
