Question

Given $y_1(x) = x$ is a solution of $y''-(\frac{2}{x^2}+\frac{1}{x})(xy'-y)=0$, $x \in (0,\infty)$, find another linearly independent solution, and hence the general solution.

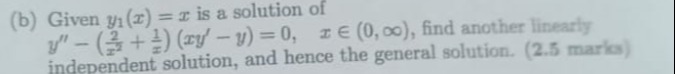
• A. Another linearly independent solution is $y_2(x) = x e^x$. The general solution is $y(x) = c_1 x + c_2 x e^x$.
• B. Another linearly independent solution is $y_2(x) = e^x$. The general solution is $y(x) = c_1 x + c_2 e^x$.
• C. Another linearly independent solution is $y_2(x) = x^2$. The general solution is $y(x) = c_1 x + c_2 x^2$.
• D. Another linearly independent solution is $y_2(x) = x^2 e^x$. The general solution is $y(x) = c_1 x + c_2 x^2 e^x$.

Answer 1

Answer: (A)

Another linearly independent solution is $y_2(x) = x e^x$. The general solution is $y(x) = c_1 x + c_2 x e^x$.

Answer 2

Let $w = xy' - y$. Then $w' = xy''$. Substituting into the ODE gives $\frac{w'}{x} - (\frac{2}{x^2}+\frac{1}{x})w = 0$. This simplifies to $w' - (\frac{2}{x}+1)w = 0$. Separating variables, $\frac{dw}{w} = (\frac{2}{x}+1)dx$. Integrating yields $\ln|w| = 2\ln x + x + K_1$, so $w = C x^2 e^x$. Substituting back $w = xy' - y$, we get $xy' - y = C x^2 e^x$, or $y' - \frac{1}{x}y = C x e^x$. The integrating factor is $\frac{1}{x}$. Multiplying by the integrating factor gives $\frac{d}{dx}(\frac{y}{x}) = C e^x$. Integrating yields $\frac{y}{x} = C e^x + K_2$, so $y(x) = K_2 x + C x e^x$. The general solution is $y(x) = c_1 x + c_2 x e^x$. Given $y_1(x) = x$, another linearly independent solution is $y_2(x) = x e^x$. The Wronskian $W(y_1, y_2) = \begin{vmatrix} x & xe^x \\ 1 & e^x+xe^x \end{vmatrix} = x(e^x+xe^x) - xe^x = x^2e^x \neq 0$ for $x \in (0,\infty)$.