Question
Question: Find the middle point of the chord intercepted on the line $2x-y+3=0$ by the ellipse $\frac{x^2}{10}...
Find the middle point of the chord intercepted on the line 2x−y+3=0 by the ellipse 10x2+6y2=1.
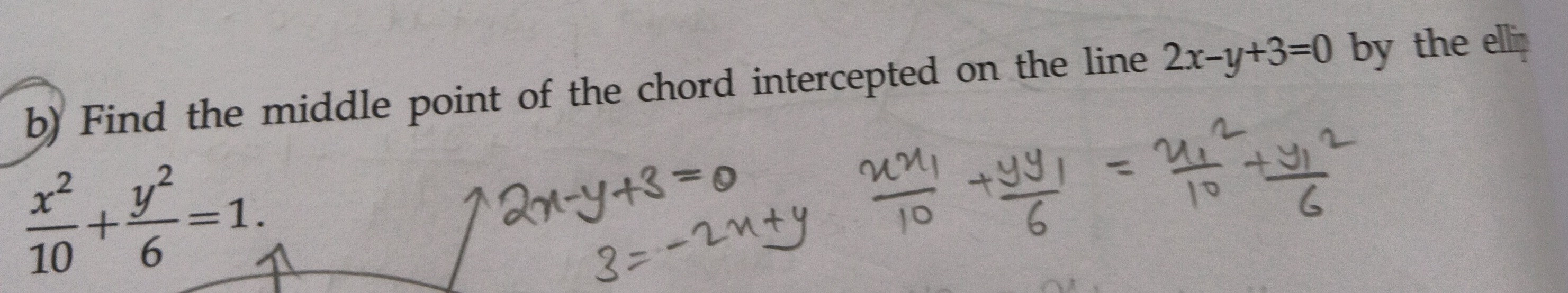
(−2330,239)
Solution
Let the middle point of the chord be (x1,y1). The equation of the chord with middle point (x1,y1) on the ellipse a2x2+b2y2=1 is given by T=S1, which is a2xx1+b2yy1=a2x12+b2y12.
In this case, a2=10, b2=6. The equation of the chord is 10xx1+6yy1=10x12+6y12.
This chord is the same as the given line 2x−y+3=0.
Comparing the coefficients of x, y, and the constant terms, we have 2x1/10=−1y1/6=3−(x12/10+y12/6).
Let the common ratio be k. Then x1=20k and y1=−6k.
Also, 3k=−(x12/10+y12/6). Substituting the expressions for x1 and y1 in terms of k, we get 3k=−(10(20k)2+6(−6k)2)=−(40k2+6k2)=−46k2.
So 46k2+3k=0, which gives k(46k+3)=0.
Since the line does not pass through the center, k=0. Thus 46k+3=0, which means k=−463.
Then x1=20k=20(−463)=−2330 and y1=−6k=−6(−463)=239.
The middle point is (−2330,239).
