Question

The image displays two separate networks of capacitors. The first network, on the left, has points labeled B and D. Between B and D, there are three capacitors with capacitances 2C, 4C, and 8C connected in series. The second network, on the right, has capacitors with capacitances 2C, 2C, 4C, and 8C connected in series. The question is asking for the equivalent capacitance of the first network between points B and D.

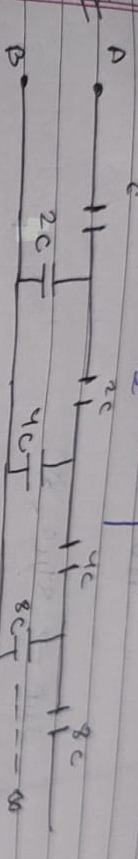
• A. B
• B. 2C
• C. 4C
• D. 8C
• E. $\infty$
• F. D
• G. C

Answer 1

$\frac{8C}{7}$

Answer 2

For capacitors connected in series, the reciprocal of the equivalent capacitance ($C_{eq}$) is the sum of the reciprocals of individual capacitances: $\frac{1}{C_{eq}} = \sum_{i} \frac{1}{C_i}$ For the first network, the capacitances are $C_1 = 2C$, $C_2 = 4C$, and $C_3 = 8C$. The equivalent capacitance $C_{BD}$ between points B and D is given by: $\frac{1}{C_{BD}} = \frac{1}{2C} + \frac{1}{4C} + \frac{1}{8C}$ To sum these fractions, we find a common denominator, which is 8C: $\frac{1}{C_{BD}} = \frac{4}{8C} + \frac{2}{8C} + \frac{1}{8C}$ $\frac{1}{C_{BD}} = \frac{4 + 2 + 1}{8C}$ $\frac{1}{C_{BD}} = \frac{7}{8C}$ Therefore, the equivalent capacitance is: $C_{BD} = \frac{8C}{7}$