Question

A force defined by the law $\overrightarrow{F}=(2xy\hat{i}+x^2\hat{j}+2\hat{k})$ N acts on a particle. The particle is shifted from the origin of the coordinate system to point C (1 m, 2 m, 4 m).

Answer 1

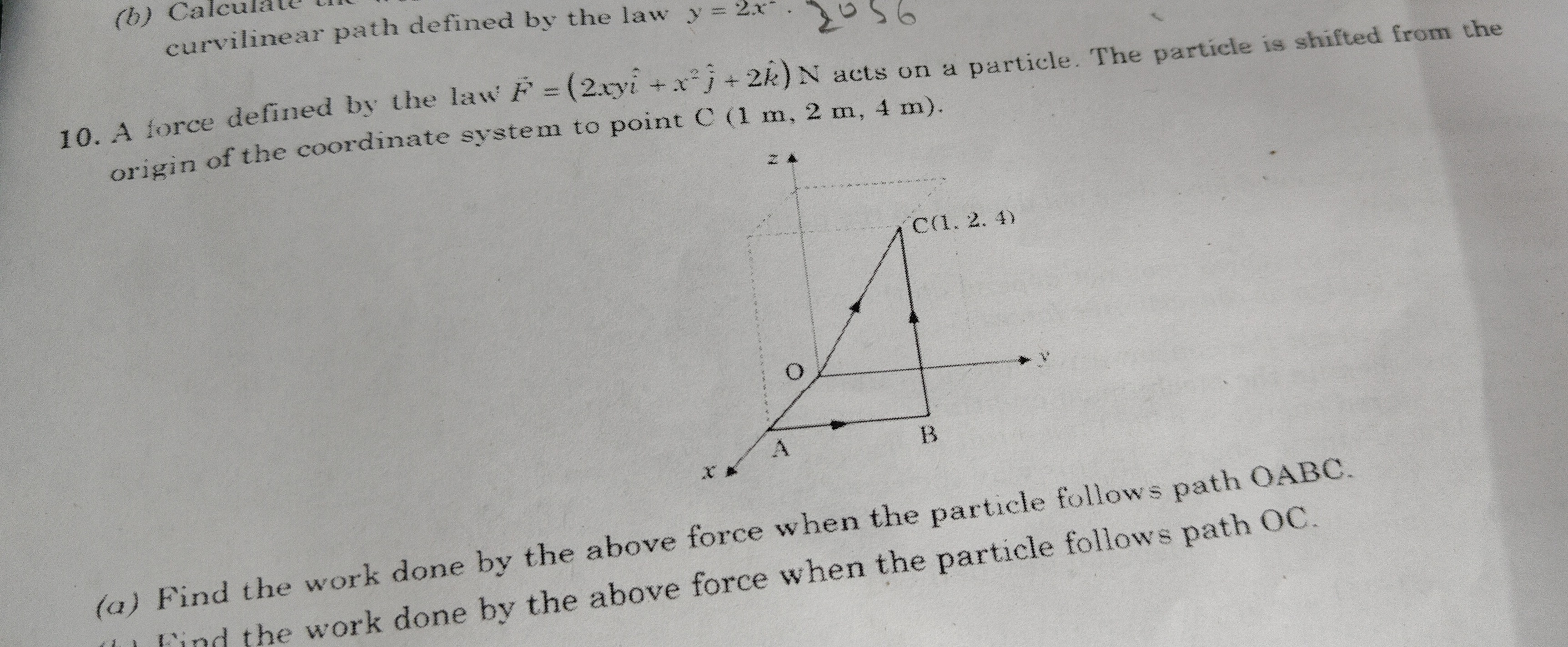
The work done by the force when the particle follows path OABC is 10 J. The work done by the force when the particle follows path OC is 10 J.

Answer 2

The problem asks to calculate the work done by a variable force $\overrightarrow{F}=(2xy\hat{i}+x^2\hat{j}+2\hat{k})$ N when a particle is shifted from the origin O (0, 0, 0) to point C (1 m, 2 m, 4 m) along two different paths.

First, let's determine if the force is conservative by calculating its curl: $\nabla \times \overrightarrow{F} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ 2xy & x^2 & 2 \end{vmatrix}$ $= \hat{i} \left( \frac{\partial(2)}{\partial y} - \frac{\partial(x^2)}{\partial z} \right) - \hat{j} \left( \frac{\partial(2)}{\partial x} - \frac{\partial(2xy)}{\partial z} \right) + \hat{k} \left( \frac{\partial(x^2)}{\partial x} - \frac{\partial(2xy)}{\partial y} \right)$ $= \hat{i} (0 - 0) - \hat{j} (0 - 0) + \hat{k} (2x - 2x)$ $= \overrightarrow{0}$

Since the curl of the force is zero, the force is conservative. This means the work done by this force depends only on the initial and final positions, not on the path taken. Therefore, the work done along path OABC should be equal to the work done along path OC.

The general formula for work done by a variable force is $W = \int \overrightarrow{F} \cdot d\overrightarrow{r}$, where $d\overrightarrow{r} = dx\hat{i} + dy\hat{j} + dz\hat{k}$. So, $\overrightarrow{F} \cdot d\overrightarrow{r} = (2xy)dx + (x^2)dy + (2)dz$.

(a) Find the work done by the above force when the particle follows path OABC.

The path OABC consists of three straight line segments: OA, AB, and BC. The coordinates are: O (0, 0, 0), A (1, 0, 0), B (1, 2, 0), C (1, 2, 4).

1. Work done along segment OA: From O (0, 0, 0) to A (1, 0, 0). Along this segment, $y=0 \implies dy=0$, $z=0 \implies dz=0$. $x$ varies from 0 to 1. $W_{OA} = \int_{x=0}^{1} (2x(0))dx + (x^2)(0) + (2)(0) = \int_{0}^{1} 0 dx = 0 \text{ J}$.

2. Work done along segment AB: From A (1, 0, 0) to B (1, 2, 0). Along this segment, $x=1 \implies dx=0$, $z=0 \implies dz=0$. $y$ varies from 0 to 2. $W_{AB} = \int_{y=0}^{2} (2(1)y)(0) + (1^2)dy + (2)(0) = \int_{0}^{2} 1 dy = [y]_{0}^{2} = 2 - 0 = 2 \text{ J}$.

3. Work done along segment BC: From B (1, 2, 0) to C (1, 2, 4). Along this segment, $x=1 \implies dx=0$, $y=2 \implies dy=0$. $z$ varies from 0 to 4. $W_{BC} = \int_{z=0}^{4} (2(1)(2))(0) + (1^2)(0) + (2)dz = \int_{0}^{4} 2 dz = [2z]_{0}^{4} = 2(4) - 2(0) = 8 \text{ J}$.

Total work done along path OABC: $W_{OABC} = W_{OA} + W_{AB} + W_{BC} = 0 + 2 + 8 = 10 \text{ J}$.

(b) Find the work done by the above force when the particle follows path OC.

The path OC is a straight line from O (0, 0, 0) to C (1, 2, 4). We can parameterize this line using a parameter $t$ from 0 to 1: $x = 0 + t(1-0) = t \implies dx = dt$ $y = 0 + t(2-0) = 2t \implies dy = 2dt$ $z = 0 + t(4-0) = 4t \implies dz = 4dt$

Substitute these into the work integral: $W_{OC} = \int_{t=0}^{1} (2(t)(2t))dt + (t^2)(2dt) + (2)(4dt)$ $W_{OC} = \int_{0}^{1} (4t^2 + 2t^2 + 8)dt$ $W_{OC} = \int_{0}^{1} (6t^2 + 8)dt$ Now, integrate with respect to $t$: $W_{OC} = \left[ \frac{6t^3}{3} + 8t \right]_{0}^{1}$ $W_{OC} = \left[ 2t^3 + 8t \right]_{0}^{1}$ $W_{OC} = (2(1)^3 + 8(1)) - (2(0)^3 + 8(0))$ $W_{OC} = (2 + 8) - 0 = 10 \text{ J}$.

As expected for a conservative force, the work done is the same for both paths.

The initial line "(b) Calculate the curvilinear path defined by the law y = 2x²." seems to be a misplaced part of another question or an incomplete statement. If it refers to calculating work done by the force in Q10 along a path from O to C where $y=2x^2$ is the projection on the xy-plane (e.g., $x=t, y=2t^2, z=4t$), the work done would also be 10 J because the force is conservative.