Question

Two spherical mirrors (convex and concave) having the same focal length of 36 cm are arranged as shown in figure so that their optical axes coincide. The separation between the mirrors is 1 m. At what distance from the concave mirror should an object be placed so that its images formed by the concave and convex mirrors independently are identical in size?

Answer 1

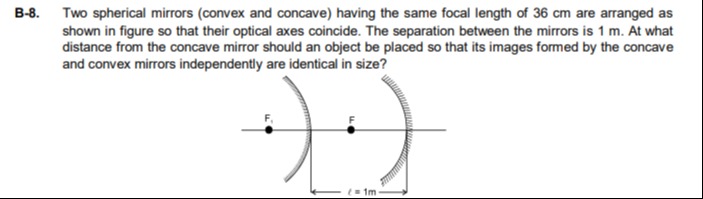
50 cm

Answer 2

To solve this problem, we need to apply the mirror formula and magnification formula for spherical mirrors.

Let the focal length of the concave mirror be $f_1 = -36$ cm.
Let the focal length of the convex mirror be $f_2 = +36$ cm.
The separation between the mirrors is $L = 100$ cm.

Let the object be placed at a distance $x$ from the concave mirror.

For the concave mirror (M1):
The object distance $u_1 = -x$. The magnification $m_1$ is given by the formula:
$m = \frac{f}{f-u}$
So, $m_1 = \frac{f_1}{f_1 - u_1} = \frac{-36}{-36 - (-x)} = \frac{-36}{-36 + x} = \frac{36}{36 - x}$.
The magnitude of magnification is $|m_1| = \left|\frac{36}{36 - x}\right|$.

For the convex mirror (M2):
The distance of the object from the convex mirror is $100 + x$.
The object distance $u_2 = -(100 + x)$.
The magnification $m_2$ is:
$m_2 = \frac{f_2}{f_2 - u_2} = \frac{36}{36 - (-(100 + x))} = \frac{36}{36 + 100 + x} = \frac{36}{136 + x}$.
The magnitude of magnification is $|m_2| = \left|\frac{36}{136 + x}\right|$.

Condition for identical image sizes:
The magnitudes of the magnifications must be equal: $|m_1| = |m_2|$.
$\left|\frac{36}{36 - x}\right| = \left|\frac{36}{136 + x}\right|$
Since the numerators are identical and positive, the magnitudes of the denominators must be equal:
$|36 - x| = |136 + x|$

This equation implies two possibilities:

Case 1: $36 - x = 136 + x$
$36 - 136 = x + x$
$-100 = 2x$
$x = -50$ cm.
This solution is not physically possible because distance $x$ cannot be negative.

Case 2: $36 - x = -(136 + x)$
$36 - x = -136 - x$
$36 = -136$
This is false, so this case yields no solution.

Re-evaluating the sign convention for the object distance for the convex mirror.
If the object is placed between the two mirrors, i.e., $0 < x < 100$ cm.
Then for the concave mirror (M1), object is at distance $x$ to its right. So $u_1 = +x$.
$m_1 = \frac{f_1}{f_1 - u_1} = \frac{-36}{-36 - x} = \frac{36}{36 + x}$.
$|m_1| = \left|\frac{36}{36 + x}\right|$.

For the convex mirror (M2), the object is at a distance $100-x$ to its left. So $u_2 = -(100-x)$.
$m_2 = \frac{f_2}{f_2 - u_2} = \frac{36}{36 - (-(100-x))} = \frac{36}{36 + 100 - x} = \frac{36}{136 - x}$.
$|m_2| = \left|\frac{36}{136 - x}\right|$.

Equating the magnitudes:
$\frac{36}{36 + x} = \left|\frac{36}{136 - x}\right|$
$\frac{1}{36 + x} = \frac{1}{|136 - x|}$
$|136 - x| = 36 + x$

Again, two possibilities for $136-x$:

Case A: $136 - x = 36 + x$
$136 - 36 = x + x$
$100 = 2x$
$x = 50$ cm.
This means the object is placed 50 cm from the concave mirror. This is between the mirrors ($0 < 50 < 100$).

For concave mirror: $u_1 = +50$ cm. $m_1 = \frac{36}{36+50} = \frac{36}{86}$. $|m_1| = \frac{36}{86}$.
For convex mirror: $u_2 = -(100-50) = -50$ cm. $m_2 = \frac{36}{136-50} = \frac{36}{86}$. $|m_2| = \frac{36}{86}$.
The magnitudes are identical. This is a valid solution.

Case B: $136 - x = -(36 + x)$
$136 - x = -36 - x$
$136 = -36$
This is false.

Therefore, the only valid position for the object is 50 cm from the concave mirror, placed between the two mirrors.