Question

(2x + 3y -1)dx - 4(x + 1)dy = 0

Answer 1

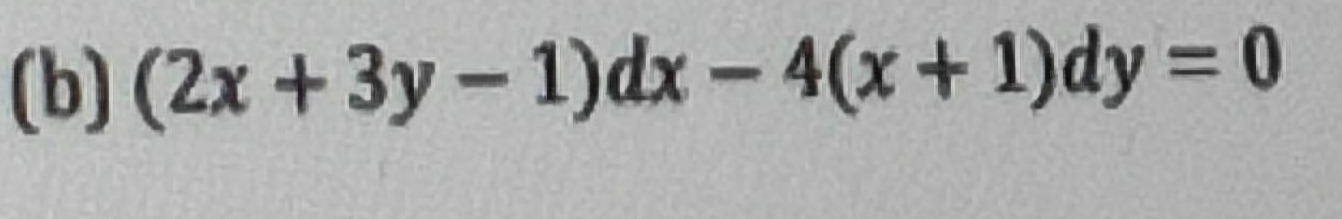
(x+1)^3 = C(2x-y+3)^4

Answer 2

The given differential equation is $(2x + 3y -1)dx - 4(x + 1)dy = 0$. We rewrite it as $\frac{dy}{dx} = \frac{2x + 3y - 1}{4(x + 1)}$. This is a first-order linear differential equation. We can solve it by making the substitution $x = X+h$ and $y = Y+k$. This gives $dx = dX$ and $dy = dY$. The equation becomes $\frac{dY}{dX} = \frac{2(X+h) + 3(Y+k) - 1}{4(X+h + 1)}$. To eliminate the constant terms, we solve the system: $2h + 3k - 1 = 0$ $h + 1 = 0 \implies h = -1$ Substituting $h = -1$ into the first equation: $2(-1) + 3k - 1 = 0 \implies -2 + 3k - 1 = 0 \implies 3k = 3 \implies k = 1$. So, we use $x = X - 1$ and $y = Y + 1$, which means $X = x+1$ and $Y = y-1$. The transformed equation is $\frac{dY}{dX} = \frac{2(X-1) + 3(Y+1) - 1}{4(X-1 + 1)} = \frac{2X - 2 + 3Y + 3 - 1}{4X} = \frac{2X + 3Y}{4X}$. This simplifies to $\frac{dY}{dX} = \frac{1}{2} + \frac{3}{4}\frac{Y}{X}$. This is a homogeneous differential equation. Let $Y = vX$, so $\frac{dY}{dX} = v + X\frac{dv}{dX}$. Substituting this gives $v + X\frac{dv}{dX} = \frac{1}{2} + \frac{3}{4}v$. $X\frac{dv}{dX} = \frac{1}{2} + \frac{3}{4}v - v = \frac{1}{2} - \frac{1}{4}v = \frac{2-v}{4}$. Separating variables: $\frac{4}{2-v}dv = \frac{1}{X}dX$. Integrating both sides: $\int \frac{4}{2-v}dv = \int \frac{1}{X}dX$. $-4\ln|2-v| = \ln|X| + C_1$. Let $C_1 = \ln|C|$. Then $-4\ln|2-v| = \ln|CX|$. $\ln|2-v|^{-4} = \ln|CX| \implies |2-v|^{-4} = |CX|$. $(2-v)^{-4} = CX$. Substitute back $v = Y/X$: $(\frac{2X-Y}{X})^{-4} = CX$. $\frac{(2X-Y)^{-4}}{X^{-4}} = CX \implies (2X-Y)^{-4} X^4 = CX \implies (2X-Y)^{-4} X^3 = C$. Substitute back $X = x+1$ and $Y = y-1$: $2X-Y = 2(x+1) - (y-1) = 2x+2 - y+1 = 2x-y+3$. The solution is $(2x-y+3)^{-4} (x+1)^3 = C$. This can be written as $\frac{(x+1)^3}{(2x-y+3)^4} = C$ or $(x+1)^3 = C(2x-y+3)^4$.