Question
Question: Average energy density of electromagnetic wave $E_y = E_0 \sin(kx - \omega t)$ and $B_z = B_0 \sin (...
Average energy density of electromagnetic wave Ey=E0sin(kx−ωt) and Bz=B0sin(kx−ωt) is given by
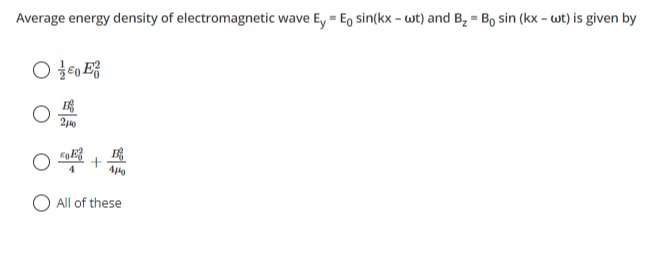
21ϵ0E02
2μ0B02
4ϵ0E02+4μ0B02
All of these
All of these
Solution
The electric field of the electromagnetic wave is given by Ey=E0sin(kx−ωt), and the magnetic field by Bz=B0sin(kx−ωt).
The instantaneous energy density due to the electric field is: ue=21ϵ0E2=21ϵ0(E0sin(kx−ωt))2=21ϵ0E02sin2(kx−ωt)
The instantaneous energy density due to the magnetic field is: um=2μ01B2=2μ01(B0sin(kx−ωt))2=2μ01B02sin2(kx−ωt)
To find the average energy density, we need to average the instantaneous energy densities over one full cycle. The average value of sin2(θ) over a full cycle is 21.
So, the average electric energy density is: ⟨ue⟩=21ϵ0E02⟨sin2(kx−ωt)⟩=21ϵ0E02×21=41ϵ0E02
The average magnetic energy density is: ⟨um⟩=2μ01B02⟨sin2(kx−ωt)⟩=2μ01B02×21=4μ01B02
The total average energy density is the sum of the average electric and magnetic energy densities: ⟨u⟩=⟨ue⟩+⟨um⟩=41ϵ0E02+4μ01B02 This matches option C.
For an electromagnetic wave in vacuum, the magnitudes of the electric and magnetic fields are related by E0=cB0, where c is the speed of light in vacuum. The speed of light is also given by c=μ0ϵ01. Therefore, E02=c2B02=(μ0ϵ01)2B02=μ0ϵ01B02. From this relation, we can write ϵ0E02=μ0B02.
Now, let's substitute this relationship into the expression for ⟨ue⟩: ⟨ue⟩=41ϵ0E02=41(μ0B02)=4μ0B02 This shows that ⟨ue⟩=⟨um⟩. The average energy density is equally divided between the electric and magnetic fields.
Using this equality, we can express the total average energy density in alternative forms:
-
In terms of E0 only: ⟨u⟩=⟨ue⟩+⟨um⟩=⟨ue⟩+⟨ue⟩=2⟨ue⟩=2(41ϵ0E02)=21ϵ0E02 This matches option A.
-
In terms of B0 only: ⟨u⟩=⟨ue⟩+⟨um⟩=⟨um⟩+⟨um⟩=2⟨um⟩=2(4μ01B02)=2μ0B02 This matches option B.
Since options A, B, and C are all correct expressions for the average energy density of an electromagnetic wave, the correct choice is "All of these".
