Question

Atoms in ${{P}_{4}}$ molecule of white phosphorus are arranged regularly in the following way:
a.) At the corners of a cube.
b.) At the corners of an octahedron.
c.) At the corners of a tetrahedron.
d.) At the center and corners of a tetrahedron.

Answer 1

The easiest way to solve this question is by calculating the hybridization of the compound given above. We generally consider the hybridization of the central element, but in this case, all the atoms will act the same, i.e. hybridization of all four phosphorus will be the same.

Complete answer:
The molecule is also known as tetraphosphorus.
Let us check the structure and geometry of white phosphorus by calculating its hybridization. Hybridization of white phosphorus can be added to the number of sigma bonds and number of lone pairs of the atom. We can represent hybridization by the term ‘Z’.
But first let us draw the structure of white phosphorus.

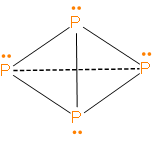
From the structure, we can clearly see that each phosphorus has 1 lone pair and 3 sigma bonds.
Therefore,
Z = Number of $\text{ }\\!\\!\sigma\\!\\!\text{ }$bonds + lone pair of phosphorus
Z = 3 + 1
Z = 4
The hybridization of white phosphorus - ${{P}_{4}}$ - is equal to 4, which means that it is $s{{p}^{3}}$ hybridized. Therefore, we can say that it is a tetrahedron.
Also, we can see from the structure that the four phosphorus atoms in white phosphorus $({{P}_{4}})$ are arranged at the corners of a regular tetrahedron.
Therefore, the answer is – option (c) – Atoms in ${{P}_{4}}$ molecules of white phosphorus are arranged regularly at the corners of a tetrahedron.
So, the correct answer is “Option C”.

Additional Information:
Hybridization is based on the concept that atomic orbitals of nearly same energy intermix to give new orbitals of the same energy.

Note:
The hybridization of a compound can be related to its geometry by the following table –

Z	Hybridization	Geometry
2	$sp$	Linear
3	$s{{p}^{2}}$	Trigonal planar
4	$s{{p}^{3}}$	Tetrahedral
5	$s{{p}^{3}}d$	Trigonal bipyramidal
6	$s{{p}^{3}}{{d}^{2}}$	Octahedral
7	$s{{p}^{3}}{{d}^{3}}$	Pentagonal bipyramidal