Question

atmospheric pressure (in torr) should be: [Given : $K_b$ of water = 0.52 K-kg/mol] 4. A solution prepared by dissolving 38.2 g of $Na_2B_4O_7 \cdot xH_2O$ in 250 g water has boiling point 100.582°C. Find the value of x in the formula of salt. [$K_b$ of the water is 0.52 K-kg mol$^{-1}$, Atomic mass of B = 11, Na = 23]

Answer 1

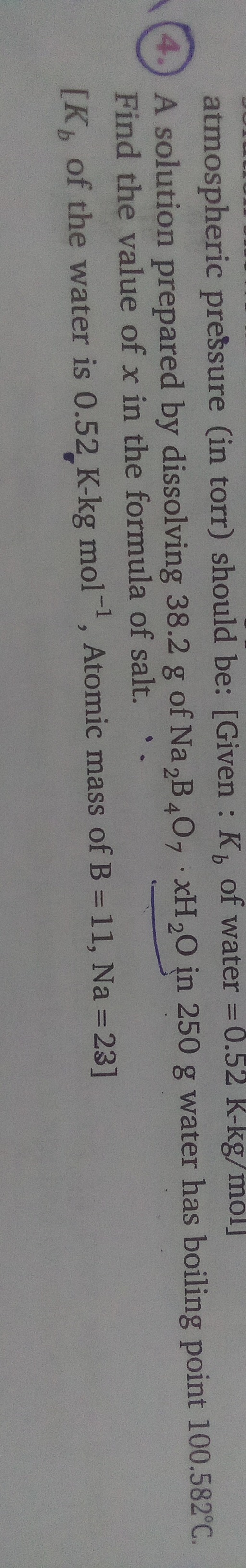
12

Answer 2

The problem asks us to find the value of 'x' in the hydrated salt $Na_2B_4O_7 \cdot xH_2O$ using the elevation in boiling point data.

Here's a step-by-step solution:

1. Calculate the elevation in boiling point ($\Delta T_b$): The boiling point of the solution is $100.582^\circ C$. The normal boiling point of pure water is $100^\circ C$. $\Delta T_b = T_b(\text{solution}) - T_b(\text{pure water})$ $\Delta T_b = 100.582^\circ C - 100^\circ C = 0.582^\circ C$ (or 0.582 K, since a change in Celsius is equal to a change in Kelvin).

2. Determine the van't Hoff factor (i) for $Na_2B_4O_7$: Sodium tetraborate ($Na_2B_4O_7$) is an ionic compound that dissociates in water. $Na_2B_4O_7(aq) \rightarrow 2Na^+(aq) + B_4O_7^{2-}(aq)$ For every one formula unit of $Na_2B_4O_7$, 2 sodium ions and 1 tetraborate ion are produced, totaling 3 ions. Therefore, the van't Hoff factor, $i = 3$.

3. Use the elevation in boiling point formula to find the molality (m) of the solution: The formula for elevation in boiling point is: $\Delta T_b = i \cdot K_b \cdot m$ Given: $\Delta T_b = 0.582$ K, $K_b = 0.52 \text{ K-kg/mol}$, $i = 3$. $0.582 = 3 \cdot 0.52 \cdot m$ $0.582 = 1.56 \cdot m$ $m = \frac{0.582}{1.56}$ $m \approx 0.3730769 \text{ mol/kg}$

4. Calculate the moles of the solute ($Na_2B_4O_7 \cdot xH_2O$): Molality (m) is defined as moles of solute per kilogram of solvent. Mass of water (solvent) = 250 g = 0.250 kg. Moles of solute = $m \times \text{Mass of solvent (in kg)}$ Moles of solute = $0.3730769 \text{ mol/kg} \times 0.250 \text{ kg}$ Moles of solute $\approx 0.0932692 \text{ mol}$

5. Calculate the experimental molar mass of the hydrated salt: Mass of $Na_2B_4O_7 \cdot xH_2O$ dissolved = 38.2 g. Molar mass = $\frac{\text{Mass of solute}}{\text{Moles of solute}}$ Molar mass $\approx \frac{38.2 \text{ g}}{0.0932692 \text{ mol}}$ Molar mass $\approx 409.56 \text{ g/mol}$

6. Calculate the theoretical molar mass of $Na_2B_4O_7 \cdot xH_2O$ in terms of x: Atomic masses: Na = 23, B = 11, O = 16, H = 1. Molar mass of $Na_2B_4O_7$: $(2 \times 23) + (4 \times 11) + (7 \times 16) = 46 + 44 + 112 = 202 \text{ g/mol}$ Molar mass of $H_2O$: $(2 \times 1) + 16 = 18 \text{ g/mol}$ Molar mass of $xH_2O = 18x \text{ g/mol}$ Total theoretical molar mass of $Na_2B_4O_7 \cdot xH_2O = 202 + 18x \text{ g/mol}$

7. Equate the experimental and theoretical molar masses and solve for x: $202 + 18x = 409.56$ $18x = 409.56 - 202$ $18x = 207.56$ $x = \frac{207.56}{18}$ $x \approx 11.531$

   Since 'x' represents the number of water molecules of crystallization, it must be an integer. Rounding $11.531$ to the nearest integer gives 12.

Explanation of the solution:

1. Calculate $\Delta T_b$ from the given boiling points.
2. Determine the van't Hoff factor ($i$) for $Na_2B_4O_7$, which dissociates into 3 ions.
3. Use the colligative property formula $\Delta T_b = i \cdot K_b \cdot m$ to find the molality ($m$).
4. Calculate the moles of solute from molality and mass of solvent.
5. Determine the experimental molar mass of the salt using its given mass and calculated moles.
6. Express the theoretical molar mass of $Na_2B_4O_7 \cdot xH_2O$ in terms of 'x' using atomic masses.
7. Equate the experimental and theoretical molar masses and solve for 'x', then round to the nearest integer.