Question
Question: At what initial speed must the basketball player in fig throw the ball, at angle \({{\theta }_{0}}={...
At what initial speed must the basketball player in fig throw the ball, at angle θ0=550 above the horizontal, to make the foul shot? The horizontal distances are d1=1.0ft and d2=14ft , and the heights are h1=7.0ft and h2=10ft.
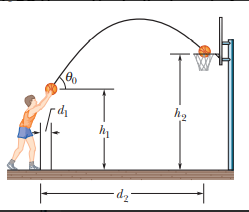
Solution
Speed is defined as the distance covered per unit time and speed is a scalar quantity. SI unit of speed is ms−1. Displacement is defined as the process in which objects' positions are changed and in displacement the initial position of objects are changed. Displacement is also defined as change in initial position of objects to the final position and displacement is denoted as S.
Complete step-by-step solution:
Displacement is a vector quantity which has both magnitude and direction and displacement is measured in terms of meters. The dimensional formula of displacement is M0L1T0 and displacement plays a very important role while determining velocity (v). Velocity is also a vector quantity.
Velocity is defined as the rate of change of displacement with respect to time and in kinematics velocity is a fundamental concept. SI unit of velocity is ms−1 and velocity tracking is the measure of velocity.
Velocity (v) =ΔtΔS
The dimensional formula of velocity is M0L1T−1.
The force which causes a change in velocity and change in velocity creates a force.
We know that
v0=cosθ0x2(xtanθ0−y)g ⋯⋯(1)
From the data g=32fts−2, x=13ft, y=3ft and θ0=550
Substituting these values in equation (1)
v0=cos550132(13tan550−3)32
We get v0=23fts−1
Note: Acceleration depends on the mass and also on the force. The force velocity, acceleration and momentum have both magnitude and a direction. Heavier objects have less acceleration compared to lighter objects. Newton’s second law of motion to relate the motion of the object to the forces involved. Objects with constant masses are used in Newton’s second law.
