Question

At what angle will a ray of light be incident on one face of an equilateral prism, so that the emergent ray may graze the second surface of the prism $\left( {\mu = 1.5} \right)$?

Answer 1

For an equilateral prism, the summation of angle of refraction at the 1st surface and angle of incident at the 2nd surface of the prism is ${60^0}$.
Apply the Snell’s law at the both surfaces to find the incident angle at the surface 1.
It states that if a ray of light passing from a medium 1 $\left( {{\mu _1}} \right)$ to another medium 2 $\left( {{\mu _2}} \right)$, then$\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
Where, $i$ and $r$ are the angles of incidence and refraction respectively.

Complete step by step answer:
Let’s draw a diagram which depicts the question.

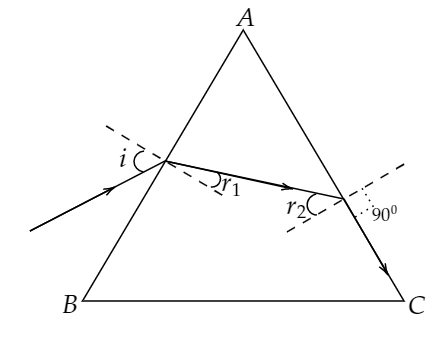
Consider a ray of light incident on the surface AB of the prism.
$i$ is the angle of incidence on the surface AB.
${r_1}$ is the angle of refraction on the surface AB.
The refracted ray from the surface AB incident on the 2nd surface AC.
${r_2}$ is the angle incidence on the surface AC.
It is given that the prism is an equilateral.
Therefore, ${r_1} + {r_2} = {60^0}$
It is also given that,
the angle refraction on the surface is ${90^0}$.
Refractive index of prism, $\mu = 1.5$
We know that the refractive index of air is $1$.
Apply the Snell’s law at the surface AC.

$\dfrac{{\sin {r_2}}}{{\sin {{90}^0}}} = \dfrac{1}{\mu }$
Further simplify
$\Rightarrow \sin {r_2} = \dfrac{1}{{1.5}}$
$\Rightarrow {r_2} = {\sin ^{ - 1}}\left( {\dfrac{1}{{1.5}}} \right)$
$\Rightarrow {r_2} = {41.81^0}$
Now ${r_1} + {r_2} = {60^0}$
$\Rightarrow {r_1} = {60^0} - {r_2}$
$\Rightarrow {r_1} = {60^0} - {41.81^0}$
Or ${r_1} = {18.19^0}$
Similarly apply Snell’s law at the surface AB.
$\dfrac{{\sin i}}{{\sin {r_1}}} = \dfrac{\mu }{1}$
$\Rightarrow \sin i = \mu \sin {r_1}$
Substitute the required values
$\Rightarrow \sin i = 1.5\sin \left( {{{18.19}^0}} \right)$
$\Rightarrow \sin i = 1.5 \times 0.312$
$\Rightarrow i = {\sin ^{ - 1}}\left( {0.468} \right)$
Or $i = {27.9^0}$
Hence, if the incident angle is ${27.9^0}$, the emergent ray will graze on the second surface AC of the prism.

Note: Note that the Refractive of a medium depends on the frequency of light. Violet color has the maximum frequency in the visible range and hence it has maximum refractive index. Therefore, the critical angle for violet color is minimum compared to other spectrums of visible light. i.e., the violet color will completely lie on the 2nd surface (AC) of the prism if the angle incident on the 1st surface (AB) is ${27.9^0}$.