Solveeit Logo
Login

Question

Question: At what angle (\(\theta \)) with the horizontal should a body be projected so that its horizontal ra...

At what angle (θ\theta ) with the horizontal should a body be projected so that its horizontal range equals the maximum height it attains?
A. θ=tan⁡−1(2)\theta = {\tan ^{ - 1}}(\sqrt 2 )
B. θ=tan⁡−1(22)\theta = {\tan ^{ - 1}}(2\sqrt 2 )
C. θ=tan⁡−1(23)\theta = {\tan ^{ - 1}}(2\sqrt 3 )
D. θ=tan⁡−1(4)\theta = {\tan ^{ - 1}}(4)

Explanation

Solution

Hint – You can start the solution by describing the general formula for calculating range and maximum height attained by the projectile i.e. R=u2sin⁡2θgR = \dfrac{{{u^2}\sin 2\theta }}{g} and hmax⁡=u2sin⁡2θ2g{h_{\max }} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} respectively. Then compare these two equations to find the angle that the projectile makes with the horizontal.

Complete step-by-step answer:
Before finding the horizontal range (the horizontal distance that the projectile covers) of the projectile, let’s describe the general formulas for calculating the horizontal range and maximum height (the maximum vertical displacement that the projectile undergoes).
The diagram for the situation given in the problem is

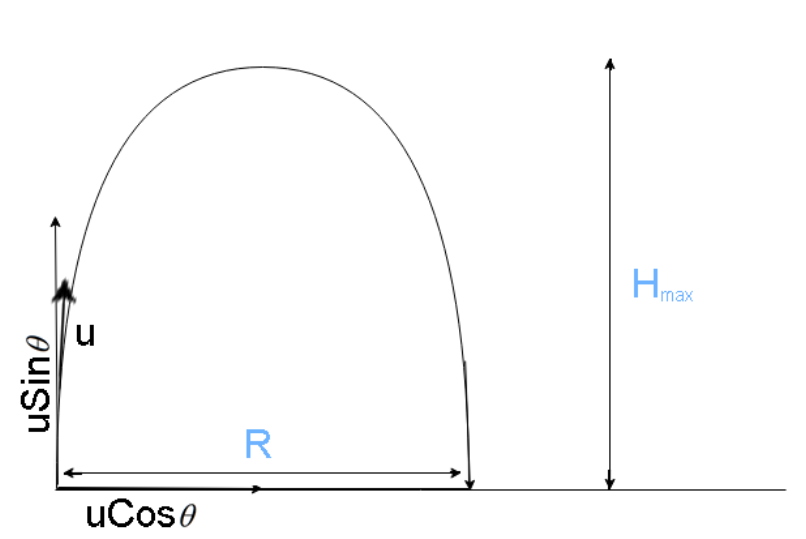
The projectile has some initial velocity (both horizontal and vertical). The horizontal velocity is not affected because there is no force affecting it, but the vertical velocity constantly decreases due to the force of gravity against it, vertical velocity is maximum at the bottom and zero at the top.
We know that
R=u2sin⁡2θgR = \dfrac{{{u^2}\sin 2\theta }}{g} (Equation 1)
And hmax⁡=u2sin⁡2θ2g{h_{\max }} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}(Equation 2)
Here
R=R = Horizontal range,
u=u = Initial speed,
θ=\theta = Angle that the projectile makes with the horizontal and
g=g = Acceleration due to gravity.
It is given in the question that the maximum height is equal to the horizontal range (R=hmax⁡R = {h_{\max }}), so by using equation 1 and 2
⇒u2sin⁡2θg=u2sin⁡2θ2g\Rightarrow \dfrac{{{u^2}\sin 2\theta }}{g} = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}
⇒sin⁡2θ=sin⁡2θ2\Rightarrow \sin 2\theta = \dfrac{{{{\sin }^2}\theta }}{2}
⇒2sin⁡θcos⁡θ=sin⁡2θ2\Rightarrow 2\sin \theta \cos \theta = \dfrac{{{{\sin }^2}\theta }}{2} (∵sin⁡2θ=2sin⁡θcos⁡θ)(\because \sin 2\theta = 2\sin \theta \cos \theta )
⇒tan⁡θ=4\Rightarrow \tan \theta = 4
θ=tan⁡−1(4)\theta = {\tan ^{ - 1}}(4)
Hence, option D is the correct choice.

Note – This problem is a classic example of projectiles, remember to always consider what the horizontal range and maximum height should be and the angle it makes with the horizontal. Like in this problem, it is clearly stated that the projectile is thrown in such a way that lets it attain horizontal range equal to the maximum height. But these conditions differ from problem to problem.