Question

At what angle should a body be projected with a velocity $24{\text{ m/s}}$ just to pass over the obstacle 14 meters high of a distance of 24 meters? (Take $g = 10{\text{ m/}}{{\text{s}}^2}$).
$A.\tan \theta = 3.8 \\\ B.\tan \theta = 1 \\\ C.\tan \theta = 3.2 \\\ D.\tan \theta = 2 \\\$

Answer 1

In this question, we need to determine the angle of projection at which the body is projected with a velocity $24{\text{ m/s}}$ just to pass over the obstacle 14 meters high of a distance of 24 meters. For this, we need to use the relation of the equation for the trajectory of the projected body.

Complete step by step answer: Let $\theta$ be the angle at which the body has been projected so that it just passes a 14 meters high obstacle, which is located at 24 meters from the point of projection.

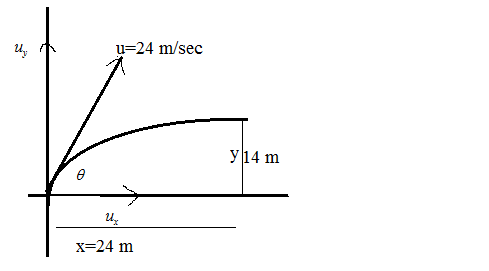
Following the equation for the trajectory path of the object, $y = x\tan \theta - \dfrac{{g{x^2}}}{{2{u^2}{{\cos }^2}\theta }}$ where,
y is the vertical displacement of the projected body (here, y=14 meters)
x is the horizontal distance traveled by the body (here, x= 24 meters)
u is the velocity of projection of the body (here, u=24 meters per second)
g is the acceleration due to gravity on the body (here, g= 10 square meters per second)
$\theta$ is the angle of projection of the body (this to be determined)

Substituting all the known values in the equation $y = x\tan \theta - \dfrac{{g{x^2}}}{{2{u^2}{{\cos }^2}\theta }}$ we get,
$y = x\tan \theta - \dfrac{{g{x^2}}}{{2{u^2}{{\cos }^2}\theta }} \\\ \Rightarrow 14 = 24\tan \theta - \dfrac{{(10){{(24)}^2}}}{{2{{(24)}^2}{{\cos }^2}\theta }} \\\$
On simplifying the above equation
$14 = 24\tan \theta - \dfrac{{(10){{(24)}^2}}}{{2{{(24)}^2}{{\cos }^2}\theta }} \\\ \Rightarrow 14 = 24\tan \theta - \dfrac{{10}}{{2{{\cos }^2}\theta }} \\\ \Rightarrow 14 = 24\tan \theta - \dfrac{5}{{{{\cos }^2}\theta }} \\\$
Now, substituting $\dfrac{1}{{{{\cos }^2}\theta }} = {\sec ^2}\theta$ in the above equation, we get
$\Rightarrow 14 = 24\tan \theta - \dfrac{5}{{{{\cos }^2}\theta }} \\\ \Rightarrow 14 = 24\tan \theta - 5{\sec ^2}\theta \\\$
Substituting ${\sec ^2}\theta = 1 + {\tan ^2}\theta$ in the above equation, we get
$\Rightarrow 14 = 24\tan \theta - 5{\sec ^2}\theta \\\ \Rightarrow 14 = 24\tan \theta - 5\left( {1 + {{\tan }^2}\theta } \right) \\\ \Rightarrow 14 = 24\tan \theta - 5 - 5{\tan ^2}\theta \\\ \Rightarrow 5{\tan ^2}\theta - 24\tan \theta + 5 + 14 = 0 \\\ \Rightarrow 5{\tan ^2}\theta - 24\tan \theta + 19 = 0 \\\$
Solving the above equation for the value of $\tan \theta$, we get
$\Rightarrow \tan \theta = \dfrac{{24 \pm \sqrt {{{\left( {24} \right)}^2} - 4(5)(19)} }}{{2(5)}} \\\ \Rightarrow \dfrac{{24 \pm \sqrt {576 - 380} }}{{10}} \\\ \Rightarrow \dfrac{{24 \pm \sqrt {196} }}{{10}} \\\ \Rightarrow \dfrac{{24 \pm 14}}{{10}} \\\ \Rightarrow \dfrac{{24 - 14}}{{10}}{\text{ and }}\dfrac{{24 + 14}}{{10}} \\\ \Rightarrow \dfrac{{10}}{{10}}{\text{ and }}\dfrac{{38}}{{10}} \\\ \Rightarrow 1{\text{ and }}3.8 \\\$

Hence, the angle of projection of the body should be $\tan \theta = 1{\text{ and tan}}\theta = 3.8$ to pass the obstacle of 14 meters height situated at 24 meters from the point of projection.
Options A and B are correct.

Note: It is interesting to note here that we got $\tan \theta = 1{\text{ and tan}}\theta = 3.8$ , i.e., two projection angles, which indicates that the body could be projected any of these two angles to pass the obstacle. Moreover, we have taken the value of acceleration due to gravity as 10 square meters per second, as it is already given in the question.