Question

At what angle does a diver see the setting sun?
a. ${41^ \circ }$to the horizon
b. ${49^ \circ }$ to the horizon
c. ${0^ \circ }$to the horizon
d. ${45^ \circ }$to the horizon

Answer 1

When attempting these questions we should keep in mind the refractive index of the mediums you are dealt with, like in this question it is explained that the diver sees the sun, so the mediums are water and air. Keep in mind that the refractive index of water is approximately $1.33$.

Complete step-by-step answer:
When we attempt this question, first thing which should come in our minds is the refractive index of water because the object we are talking about is a diver, and he is looking at the sun through water.
So, ${u_w}$=$\dfrac{4}{3}$ which is approximately $1.33$
Also keep in mind the various trigonometric equations relating to sin, cosine and tan because these equations are used in various forms multiple times in questions like the one we are dealing with right now.
Now since the angle of refraction is${90^ \circ }$, we can assume the angle of incidence to be the critical angle.
Optically speaking, critical angle is the angle where a ray of light travelling in one transparent medium, strikes the boundary between that medium and a second medium which has a lower refractive index without being totally reflected within the first medium.

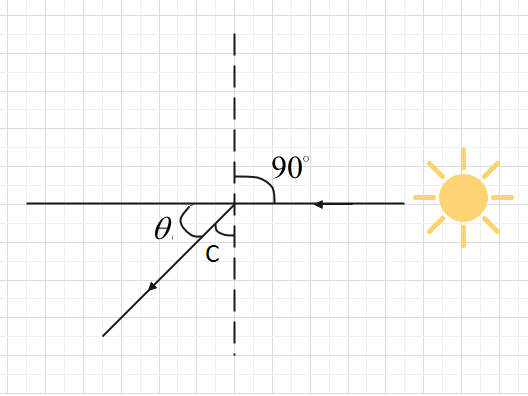
In this diagram, we are denoting the critical angle by $C$so we get,
Angle of incidence $\angle i = \angle C$
Now let’s talk about Snell’s law. When we talk about optics we talk about Snell’s law. It is basically talking about a relationship between the path taken by a ray of light when crossing the boundary or surface of separation between two contacting surfaces and the refractive index of each.
Here the two contacting surfaces are water and air and we already know their refractive index.
Snell’s law basically says, that if you have two refractive indexes ${n_1}$and ${n_2}$and the angles of incidence that the ray makes with normal is $\sin {a_1}$ and $\sin {a_2}$then
$\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{\sin {a_2}}}{{\sin {a_1}}}$
This on rearranging also turns out to be-
${n_1} \times \sin {a_1} = {n_2} \times \sin {a_2}$
So if we put in values,
$1 \times \sin {90^ \circ } = {u_w} \times \sin C$
We know ${u_w}$=$\dfrac{4}{3}$
\Rightarrow $$$$1 = \dfrac{4}{3}\sin C
\Rightarrow $$$$C = {\sin ^{ - 1}}(\dfrac{3}{4})
We know ${\sin ^{ - 1}}(\dfrac{3}{4}) = {49^ \circ }$
Therefore, $\angle C = {49^ \circ }$
Therefore $\theta = {90^ \circ } - {49^ \circ } = {41^ \circ }$

So, the correct answer is “Option A”.

Note: Refraction is the bending of light when it passes from one medium to another. We have talked about Snell’s law which is one of the two laws of refraction which states that the ratio of sine of angle of incidence to the sine of angle of refraction is constant. The other law is that the incident ray, refracted ray and the normal all lie in the same plane.