Question

At what angle a ball should be thrown with a velocity of $24{\text{ }}m{s^{ - 1}}$ just to cross a wall $16{\text{ }}m$ high at a horizontal distance of $32{\text{ }}m$. Given $g = 10{\text{ }}m{s^{ - 2}}$.

Answer 1

The motion of the ball is in projectile. We have to formulate equations for both horizontal direction and vertical direction. Then by solving the equation we will formulate another quadratic equation, from which we will find the value of angle of projection.

Complete step by step answer:

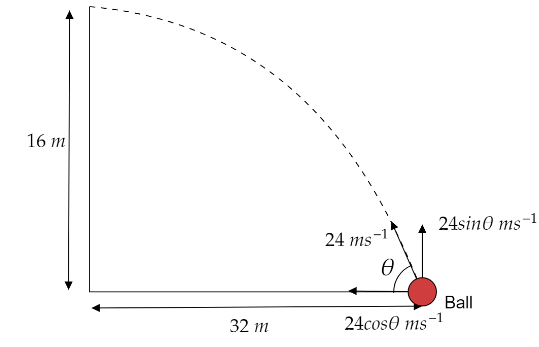
According to the question the ball has to just cross the height $16{\text{ }}m$.
So, we consider the height $y = 16{\text{ }}m$.
Let the horizontal distance be $x$ which is given as $32{\text{ }}m$.
The velocity of the particle $u$ is given as $24{\text{ }}m{s^{ - 1}}$.

Let $\theta$ be the angle of inclination.So, the horizontal velocity is $24\cos \theta$ and the vertical velocity is $24\sin \theta$. Let us formulate the equation for horizontal axis as,
$s = ut + \dfrac{1}{2}a{t^2}$ where $s = x = 32{\text{ }}m$, $u = 24\cos \theta$ and $a = 0$ for horizontal direction in projectile motion.
Substituting the values we get,
$32 = 24\cos \theta \times t$
Formulating the equation terms of $t$ we get,
$t = \dfrac{4}{3}\sec \theta - - - - - \left( 1 \right)$

Now, its time to formulate the equation in vertical axis,
$s = ut + \dfrac{1}{2}a{t^2}$ where $s = y = 16{\text{ }}m$, $u = 24\sin \theta$, $a = - g = - 10{\text{ }}m{s^{ - 2}}$
So, by substituting the values in the equation we get,
$16 = 24\sin \theta \times t - \dfrac{1}{2} \times 10 \times {t^2}$
Substituting the value of $t$ from equation $\left( 1 \right)$ we get,
$16 = 24\sin \theta \times \dfrac{4}{3}\sec \theta - \dfrac{1}{2} \times 10 \times {\left( {\dfrac{4}{3}\sec \theta } \right)^2}$
Simplifying the equation we get,
$16 = 32\tan \theta - \dfrac{{80}}{9}{\sec ^2}\theta$
Converting ${\sec ^2}\theta = 1 + {\tan ^2}\theta$ and dividing the whole equation with $16$ we get,
$\Rightarrow 1 = 2\tan \theta - \dfrac{5}{9}\left( {1 + {{\tan }^2}\theta } \right)$

Again, simplifying the equation we get,
$9 = 18\tan \theta - 5 - 5{\tan ^2}\theta$
By, arranging the equation in quadratic form we get,
$5{\tan ^2}\theta - 18\tan \theta + 14 = 0$
From Sreedhar Acharya’s formula we get,
$\tan \theta = \dfrac{{18 \pm \sqrt {324 - 4 \times 5 \times 14} }}{{2 \times 5}} = \dfrac{{18 \pm \sqrt {44} }}{{10}}$
Thus we get the values of $\tan \theta$ while considering positive value is,
$\tan \theta = 2.4633$
While considering negative value we get,
$\therefore \tan \theta = 1.1367$

Thus, the values of $\theta$ are ${23.24^ \circ }$ and ${50.39^ \circ }$.

Note: It must be noted that in order the ball should just cross the wall the angle must be a little greater than either ${23.24^ \circ }$ or ${50.39^ \circ }$. We consider the uniform motion of a body in projectile motion so the acceleration in the horizontal axis is zero.