Solveeit Logo
Login

Question

Question: At time $t=0$, a battery of 10 V is connected across points $A$ and $B$ shown in figure. If the capa...

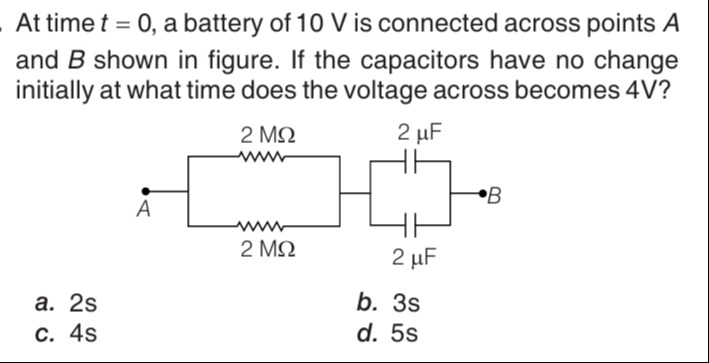
At time t=0t=0, a battery of 10 V is connected across points AA and BB shown in figure. If the capacitors have no change initially at what time does the voltage across becomes 4V?

A

2s

B

3s

C

4s

D

5s

Answer

2s

Explanation

Solution

The circuit consists of two resistors of 2 MΩ2 \text{ MΩ} in parallel, and two capacitors of 2 μF2 \text{ μF} in parallel.

The equivalent resistance of the two parallel resistors is Req=2 MΩ×2 MΩ2 MΩ+2 MΩ=4 (MΩ)24 MΩ=1 MΩ=1×106 ΩR_{eq} = \frac{2 \text{ MΩ} \times 2 \text{ MΩ}}{2 \text{ MΩ} + 2 \text{ MΩ}} = \frac{4 \text{ (MΩ)}^2}{4 \text{ MΩ}} = 1 \text{ MΩ} = 1 \times 10^6 \text{ Ω}.

The equivalent capacitance of the two parallel capacitors is Ceq=2 μF+2 μF=4 μF=4×10−6 FC_{eq} = 2 \text{ μF} + 2 \text{ μF} = 4 \text{ μF} = 4 \times 10^{-6} \text{ F}.

When a battery of voltage V0=10 VV_0 = 10 \text{ V} is connected across points A and B at time t=0t=0, the voltage across the capacitors as a function of time is given by the formula for charging an RC circuit:

VC(t)=V0(1−e−t/τ)V_C(t) = V_0 (1 - e^{-t/\tau})

where τ\tau is the time constant of the circuit, given by τ=ReqCeq\tau = R_{eq} C_{eq}.

Calculate the time constant τ\tau:

τ=ReqCeq=(1×106 Ω)×(4×10−6 F)=4 s\tau = R_{eq} C_{eq} = (1 \times 10^6 \text{ Ω}) \times (4 \times 10^{-6} \text{ F}) = 4 \text{ s}.

We are given that the voltage across the capacitors becomes VC(t)=4 VV_C(t) = 4 \text{ V}. We need to find the time tt when this occurs.

Substitute the given values into the equation:

4 V=10 V(1−e−t/4)4 \text{ V} = 10 \text{ V} (1 - e^{-t/4})

Divide both sides by 10:

0.4=1−e−t/40.4 = 1 - e^{-t/4}

Rearrange the equation to solve for e−t/4e^{-t/4}:

e−t/4=1−0.4=0.6e^{-t/4} = 1 - 0.4 = 0.6

Take the natural logarithm of both sides:

−t/4=ln⁡(0.6)-t/4 = \ln(0.6)

t=−4ln⁡(0.6)t = -4 \ln(0.6)

Using the property ln⁡(a)=−ln⁡(1/a)\ln(a) = -\ln(1/a), we have ln⁡(0.6)=ln⁡(3/5)=−ln⁡(5/3)\ln(0.6) = \ln(3/5) = -\ln(5/3).

So, t=−4(−ln⁡(5/3))=4ln⁡(5/3)t = -4 (-\ln(5/3)) = 4 \ln(5/3).

Now we need to evaluate 4ln⁡(5/3)4 \ln(5/3).

Using approximate values, ln⁡(5/3)=ln⁡(1.666...)\ln(5/3) = \ln(1.666...).

ln⁡(5)≈1.6094\ln(5) \approx 1.6094 and ln⁡(3)≈1.0986\ln(3) \approx 1.0986.

ln⁡(5/3)=ln⁡(5)−ln⁡(3)≈1.6094−1.0986=0.5108\ln(5/3) = \ln(5) - \ln(3) \approx 1.6094 - 1.0986 = 0.5108.

t≈4×0.5108=2.0432 st \approx 4 \times 0.5108 = 2.0432 \text{ s}.

The calculated value 2.0432 s is closest to 2s.