Question

At the moment $t = 0$ the force $F = at$ is applied to a small body of mass m resisting on a smooth horizontal plane (a is constant). The permanent direction of this forms an angle $\alpha$ with the horizontal. Find:
a) The velocity of the body at the moment of its breaking off the plane.
b) The distance traversed by the body up to this moment.

Answer 1

The differentiation of the acceleration with respect to time gives velocity, the differentiation of the velocity with respect to time gives displacement. The force on the body depends upon the time and therefore the force on the body was initially zero.

Formula used: The velocity is given by,
$\dfrac{{da}}{{dt}} = v$.
Where acceleration is a velocity is v and time taken is t.
The displacement is given by,
$\dfrac{{dv}}{{dt}} = s$.
Where velocity is v displacement is s and time taken is t.

Complete step by step answer:
It is given in the problem that at $t = 0$ the force $F = at$ is applied to a small body of mass m resting on a smooth horizontal plane where a is constant we need to find the velocity of the body at the moment when the body leaves the ground and also the distance travelled by body up to this moment if the angle of applied force from horizontal is $\alpha$.

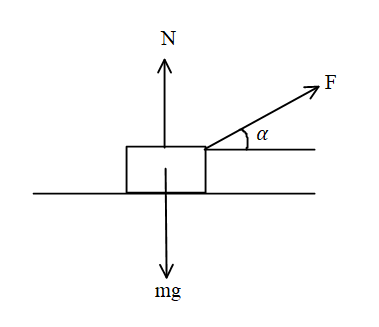
The normal reaction will be zero where the body will leave the ground surface.
$\Rightarrow N = mg - a{t_o}\sin \alpha$
$\Rightarrow mg - a{t_o}\sin \alpha = 0$
$\Rightarrow {t_o} = \dfrac{{mg}}{{a\sin \alpha }}$………eq. (1)
Where ${t_o}$ is the time when the body leaves the ground.
The force component on horizontal direction is equal to,
$\Rightarrow m{a_x} = at\cos \alpha$………eq. (2)
Since, ${a_x} = \dfrac{{d{v_x}}}{{dt}}$
Replacing the value of ${a_x}$ in equation (2).
$\Rightarrow m{a_x} = at\cos \alpha$
$\Rightarrow m \cdot \left( {\dfrac{{d{v_x}}}{{dt}}} \right) = a\cos \alpha \cdot t$
$\Rightarrow m \cdot \int\limits_0^v {d{v_x}} = a\cos \alpha \cdot \int\limits_0^{{t_o}} {tdt}$
$\Rightarrow m \cdot v = a\cos \alpha \cdot \left( {\dfrac{{{t_o}^2}}{2}} \right)$
$\Rightarrow v = \dfrac{{a\cos \alpha \cdot {t_o}^2}}{{2 \cdot m}}$………eq. (3)
Replace the value of ${t_o}$ from equation (1) to equation (3).
$\Rightarrow v = \dfrac{{a\cos \alpha \cdot {t_o}^2}}{{2 \cdot m}}$
$\Rightarrow v = \left( {\dfrac{{a\cos \alpha }}{{2 \cdot m}}} \right) \cdot {\left( {\dfrac{{mg}}{{a\sin \alpha }}} \right)^2}$
$\Rightarrow v = \left( {\dfrac{{a\cos \alpha }}{{2 \cdot m}}} \right) \cdot \left( {\dfrac{{{m^2}{g^2}}}{{{a^2}{{\sin }^2}\alpha }}} \right)$
$\Rightarrow v = \left( {\dfrac{{\cos \alpha }}{2}} \right) \cdot \left( {\dfrac{{m{g^2}}}{{a{{\sin }^2}\alpha }}} \right)$
$\Rightarrow v = \left( {\dfrac{{m{g^2}}}{{2 \cdot a \cdot \sin \alpha \cdot \tan \alpha }}} \right)$
From equation,
$\Rightarrow v = \dfrac{{a\cos \alpha \cdot {t_o}^2}}{{2 \cdot m}}$
Since, $\dfrac{{ds}}{{dt}} = {v_x}$
$\Rightarrow v = \dfrac{{a\cos \alpha \cdot {t_o}^2}}{{2 \cdot m}}$
$\Rightarrow \dfrac{{ds}}{{dt}} = \dfrac{{a\cos \alpha \cdot {t_o}^2}}{{2 \cdot m}}$
$\Rightarrow \int\limits_0^s {ds} = \dfrac{{a\cos \alpha }}{{2 \cdot m}} \cdot \int\limits_0^{{t_o}} {{t^2}} dt$
$\Rightarrow s = \dfrac{{a\cos \alpha \cdot {t_o}^3}}{{6 \cdot m}}$.
The velocity of the body at point where the body leaves the ground is equal to$v = \dfrac{{m{g^2}}}{{2 \cdot a \cdot \sin \alpha \cdot \tan \alpha }}$.
The displacement of the body till the body leaves the ground is$s = \dfrac{{a\cos \alpha \cdot {t_o}^3}}{{6 \cdot m}}$.

Note: It is advisable for students to understand and remember the concept of differentiation of the physical quantities and the results that we obtain. Force applied on anybody will change the acceleration of the body and if the force is at an angle from the horizontal then the vertical component of the force will decrease the net weight of the body.