Question

At the height of 80 m, an airplane is moving with 150 m/s. A bomb is dropped from it so as to hit a target. At what distance from the target should the bomb be dropped?
(Given$g = 10\,{\text{m/}}{{\text{s}}^2}$)
A. 605.3 m
B. 600 m
C. 80 m
D. 230 m

Answer 1

Using a kinematic equation, determine the time taken by the bomb to hit the target. Then determine the horizontal distance travelled by the bomb by using the kinematic equation in the horizontal direction. Refer to the geometry of the motion of the bomb to calculate the total distance travelled by the bomb.

Formula used:
$s = ut + \dfrac{1}{2}a{t^2}$
Here, s is the displacement, $u$ is the initial vertical velocity, g is the acceleration due to gravity and t is the time.

Complete step by step answer:
We have given the velocity of airplane is $v = 150\,{\text{m/s}}$ and therefore, the initial velocity of the bomb will the velocity of the airplane that is ${u_b} = 150\,{\text{m/s}}$.
Let’s draw the motion of the bomb as shown in the figure below.

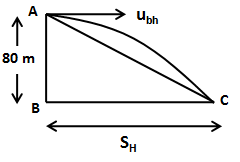
In the above figure, ${u_{bh}}$ is the initial horizontal velocity of the bomb and ${S_H}$ is the horizontal distance travelled by the bomb.
The total distance covered by the bomb is AC.
We can use the kinematic equation to determine the time taken by the bomb to hit the target as follows,
${S_V} = {u_{bv}}t + \dfrac{1}{2}g{t^2}$
Here, ${u_{bv}}$ is the initial vertical velocity of the bomb, g is the acceleration due to gravity and t is the time.
Since the beginning, the bomb has only a horizontal component of velocity. Therefore, the initial vertical velocity of the bomb is zero.
${S_V} = \dfrac{1}{2}g{t^2}$
$\Rightarrow t = \sqrt {\dfrac{{2{S_V}}}{g}}$
Substituting 80 m for ${S_V}$ and $10\,{\text{m/}}{{\text{s}}^2}$ for g in the above equation, we get,
$t = \sqrt {\dfrac{{2\left( {80} \right)}}{{10}}}$
$\Rightarrow t = 4\,{\text{s}}$
Now, we can use the kinematic equation in the horizontal direction of motion of the bomb to determine the horizontal distance ${S_H}$.
${S_H} = {u_{bh}}t$
Substituting 150 m/s for ${u_{bh}}$ and 4 s for t in the above equation, we get,
${S_H} = \left( {150} \right)\left( 4 \right)$
$\Rightarrow {S_H} = 600\,{\text{m}}$
Now, from the geometry of the above figure, we can calculate the distance AC as,
$AC = \sqrt {S_V^2 + S_H^2}$
Substituting 80 m for ${S_V}$ and 600 m for ${S_H}$ in the above equation, we get,
$AC = \sqrt {{{\left( {80} \right)}^2} + {{\left( {600} \right)}^2}}$
$\Rightarrow AC = 605.3\,{\text{m}}$

Therefore, the bomb has to be dropped 605.3 m from the target.

So, the correct answer is “Option A”.

Note:
While solving these types of questions, the direction of motion is very important. For the downward motion, the acceleration due to gravity, distance and velocity should be negative. The bomb dropped from the airplane will follow the projectile motion and therefore, the distance AC that we have calculated will be slightly less than the original distance covered by the bomb.