Question

At the end of the school day, student A and student B say goodbye and head in opposite directions, walking at constant rates. Student B heads west to the bus stop, while student A walks east to her house. After 3.0 min, student A is 300 m east and student B is 450 m west. Assuming east to be the positive direction, the velocities in m/s of student A and student B are:

A. +1.67 m/s; -2.5m/s
B. +1.67m/s; +2.5m/s
C. +2.5 m/s; -1.67 m/s
D. -1.67 m/s; +2.5m/s

Answer 1

In order to solve this problem we need to know that 1 min is 60 seconds and velocity is equal to distance travelled in meters upon time taken in seconds. Drawing the coordinate axes will help us to get the right direction including signs. Doing this will solve your problem.

Complete answer:
So, the figure for this problem can be drawn as;

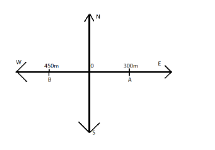
This figure is when the students A and B arrived there home and bus stop after three minutes.
We know that 1 minute = 60 seconds.
Therefore 3 minutes = 180seconds.
So, after 3 min A travels 300m east that is in a positive direction.
We know that velocity is distance upon time, so we get velocity.
$\Rightarrow \dfrac{{300}}{{180}} = 1.67$m/s in a positive direction.
So, after 3 min B travels 450m west that is in a negative direction.
We know that velocity is distance upon time, so we get velocity.
$\Rightarrow \dfrac{{450}}{{180}} = 2.5$m/s in negative direction.
So, the correct answer is +1.67m/s and -2.5m/s.

So, the correct answer is “Option A”.

Note:
When you get to solve such problems you need to know that velocity is equal to distance upon time and always consider direction in velocity since it is a vector quantity and must be written with direction. You also need to know that SI unit of velocity is m/s that is meter per second and we have given the answer in meter per second since the options are in meter per second. Most of the time we have to give an answer in the SI unit after converting all the terms in the SI unit. Doing this will help you further and will give you the right answer.