Question
Question: At the centre of the square A. E=0, V=0 B. \(E\ne 0\), V=0 C. E=0,\(V\ne 0\) D. \(E\ne 0,V\...
At the centre of the square
A. E=0, V=0
B. E=0, V=0
C. E=0,V=0
D. E=0,V=0
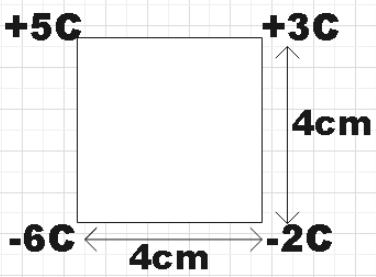
Solution
As a first step, you could think of the differences between the two given quantities. Also, give a brief description about both. Now find the net potential and electric field due to these charges by considering the direction and sign as per requirement. Thus, determine which among the given options is true.
Formula used:
Electric field,
E=r2kQ
Electric potential,
V=rkQ
Complete Step by step solution:
In the question, we are given four charges that are kept at the four corners of the square. The charges are +5C, +3C, -6C and -2C. The side of the square is given as 4cm. By using this information, we are supposed to find which among conditions given in the options is correct.
In order to find the answer to the question, we have to first understand what exactly electric potential and electric fields are. The electric field E due to some charge Q is given by,
E=r2kQ
The electric field is a vector quantity and thus for a system of charges, the net field would be the vector sum of these electric fields. The field due to positive charge would be directed away from it and that due to negative charge will be directed towards it.
Clearly, by doing the vector sum of the fields due to the given charges, we will get a non zero value.
Hence, E=0
Now the potential is given by,
V=rkQ
Electric potential being a scalar, net potential can be given by the sum of the potentials due to individual charges.
Vnet=(42)25k+(42)23k−(42)26k−(42)22k
∴Vnet=0
Therefore, we found option B to be the correct answer.
Note:
You may have noted the constant k that we repeatedly used in every equation in the solution. This constant is known to have the value,
k=4πε01=9×109Nm2C−2
The electric potential can be defined as the work done to move unit electric charge from one point to the other. Electric field can be described as the gradient of electrostatic potential.
