Question

At the Centre of the ring, the ${E_{centre}} =$

A. $\dfrac{{kQ}}{R}$
B. $0$
C. $\dfrac{{kQ}}{{{R^2}}}$
D. $\dfrac{{kQ}}{{{R^3}}}$

Answer 1

In order to solve this question you have to know the concept of electric field intensity of the ring. For this question, you have to take a small charge on the ring and find the electric field on that and then integrate it for the whole ring.

Complete step by step solution:
Let us assume that the total charge on the ring is given by $Q$
And also consider a small charge element on the ring of charge $dq$

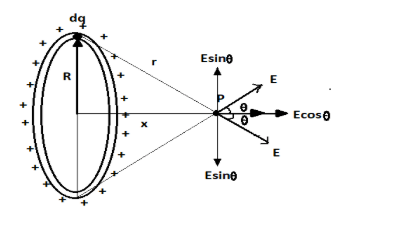
So the value of $dq$ is given by,

$dq = \dfrac{Q}{{2\pi R}}$

Now, the electric field intensity at point P due to this $dq$ element is given by,

$E = \dfrac{{kdq}}{{{r^2}}}$ ………(i)

Where, $r$ is the distance between the point P and the small charge $dq$
Now, in the triangle given in the above diagram, use Pythagoras theorem,

${r^2} = {R^2} + {x^2}$ ………(ii)

On putting the above value in the equation (i), we get

$E = \dfrac{{kdq}}{{({R^2} + {x^2})}}$

Now, from the above figure we can see that the electric field component perpendicular to the axis is cancelled by two diametrically opposite points.
Hence, the component of electric field along the axis is left which generates the electric field.

${E_{net}} = \int {E\cos \theta }$

Now put the value of electric field intensity in the above equation,

$\Rightarrow {E_{net}} = \int {\dfrac{{k\cos \theta }}{{({R^2} + {x^2})}}dq}$

Now integrate the above value, we get

$\Rightarrow {E_{net}} = \dfrac{{kQ}}{{({R^2} + {x^2})}}\cos \theta$ ……….(iii)

Now from the triangle in the above diagram, we get

$\cos \theta = \dfrac{x}{r}$

Now put the value of $r$ from the equation (ii)

$\cos \theta = \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}$

Put that above value in the equation (iii),

$\Rightarrow {E_{net}} = \dfrac{{kQ}}{{({R^2} + {x^2})}}\dfrac{x}{{\sqrt {{R^2} + {x^2}} }}$

On further solving, we get

$\Rightarrow {E_{net}} = \dfrac{{kQx}}{{{{({R^2} + {x^2})}^{3/2}}}}$

In this question, we have to find the electric field intensity at the centre. Thus, at centre, $x = 0$
Hence, put $x = 0$ in the above equation, we get

${E_{net}} = 0$
Hence, the electric field intensity at the centre is zero.

Therefore, the correct option is (B).

Note: Electric field is the space around an electric charge in which its influence can be felt. And the electric field intensity at a point can be defined as the force experienced by a unit charge placed at that point. It is a vector quantity and its unit is $N{C^{ - 1}}$ or $V{m^{ - 1}}$. Also remember that due to the positive charge, the electric field intensity is always directed away from the charge and due to the negative charge, it is towards the charge.