Question

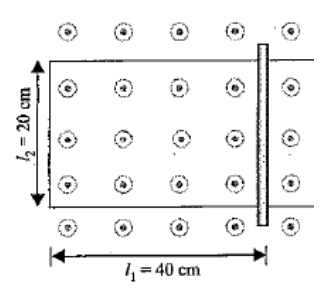
$At\;t = 0$, when the magnetic field is switched on, the conducting rod is moved to the left at a constant speed of $5\;cm$ ${s^{ - 1}}$ by some external means. The rod moves perpendicular to the rail.$At\;t = 2\;s$, induced emf has magnitude

(A) ${\mathbf{0}}.{\mathbf{12V}}$
(B) ${\mathbf{0}}.{\mathbf{08V}}$
(C) ${\mathbf{0}}.{\mathbf{04V}}$
(D) ${\mathbf{0}}.{\mathbf{02V}}$

Answer 1

To solve this question,we must have knowledge of Faraday’s law of induction, Lenz’s law and relation to the Faraday’s law. We should also know about vector calculus.

Complete step by step answer:
An emf can be induced in a coil if the magnetic flux through the coil is changed. It also makes a difference how fast the change is; a quick change induces more emf than a gradual change. This is summarized in Faraday's law of induction. The induced emf in a coil of N loops produced by a change in flux in a certain time interval is given by:
Faraday's law of induction,
$\varepsilon = - N\dfrac{{\Delta \phi }}{{\Delta t}}$
Recalling that the flux through a loop of area A is given by
$\phi = BA\cos \phi$
Faraday's law can be written:
$\varepsilon = - N\dfrac{{\Delta \left( {BA\cos \phi } \right)}}{{\Delta t}}$
The negative sign in Faraday's law comes from the fact that the emf induced in the coil acts to oppose any change in the magnetic flux. This is summarized in Lenz's law.
Lenz's law: The induced emf generates a current that sets up a magnetic field which acts to oppose the change in magnetic flux.
Another way of stating Lenz's law is to say that coils and loops like to maintain the status quo$\left( {i.e.,{\text{ }}they{\text{ }}don't{\text{ }}like{\text{ }}change} \right)$. If a coil has zero magnetic flux, when a magnet is brought close then, while the flux is changing, the coil will set up its own magnetic field that points opposite to the field from the magnet. On the other hand, a coil with a particular flux from an external magnetic field will set up its own magnetic field in an attempt to maintain the flux at a constant level if the external field $\left( {and{\text{ }}therefore{\text{ }}flux} \right)$ is changed.
By applying Faraday's law of induction,
Induced emf$\varepsilon$,

$$\varepsilon = \dfrac{{d\left( {BA} \right)}}{{dt}} \\\ \varepsilon = {I_1}{I_2}\dfrac{{dB}}{{dt}} + {I_2}B\dfrac{{d{I_1}}}{{dt}} \\\ \varepsilon = {I_1}{I_2}(2) - {I_2}Bv \\\$$

$At{\text{ }}t{\text{ }} = {\text{ }}2{\text{ }}sec$

{I_1} = \left\\{ {0.4 - \left( {0.5 \times 0.2} \right)} \right\\} = 0.3 \\\ B = 2(2) = 4 \\\ \varepsilon = \left\\{ {\left( {0.3 \times 0.2 \times 2} \right) - \left( {0.2 \times 4 \times 0.05} \right)} \right\\} = 0.08V \\\

So, the correct Option is (B)

Note: Sometimes students forgot to include the negative sign which is present in Faraday’s second of electromagnetic induction and this would result in taking the wrong direction of the induced emf so be kept this point in your mind.