Question

At polarizing angle, the angle between the reflected ray and the refracted ray is ___.

Answer 1

Hint: First define the polarizing angle. Then we will see the reflection amplitude coefficient for different angles of incidence. Use the formula, $r_{||}=-\dfrac{\tan(i-r)}{\tan(i+r)}$ and finally, we can find the required angle between the refracted and the reflected ray of light.
Formula used: $r_{||}=-\dfrac{\tan(i-r)}{\tan(i+r)}$

Complete step by step solution:
Light normally has its electric vector oriented at any direction normal to the direction of its motion. Such a ray is said to be unpolarized.
But, when the electric vector of the ray of light is in a particular plane that’s containing the propagation vector of the light, therefore the light is said to be polarized.
It was found that when light falls on the surface of some substance, there is a particular angle of incidence for which the reflected ray is totally polarized. This incidence angle is called the polarizing angle.
In this case, the light components for which the electric vector is perpendicular to the plane of paper, is totally reflected. But the components that have light vectors along the plane of the paper are not reflected.
If $r_{||}$ be the ratio of reflected amplitude to the incident amplitude for the reflected rays with electric vector parallel to the plane of the paper, we have the formula,
$r_{||}=-\dfrac{\tan(i-r)}{\tan(i+r)}$
Here, ‘I’ is the angle of incidence of light and ‘r’ is the angle of refraction of light.
Now, plainly at the polarizing angle, $r_{||}$ is equal to zero.
Now, to have this condition satisfied, we look at the formula and find that it’s possible when $(i+r)=90^\circ$.
For this $\tan(i+r)$ tends to infinity and the value of $r_{||}$ becomes zero. Now, look at the diagram given,

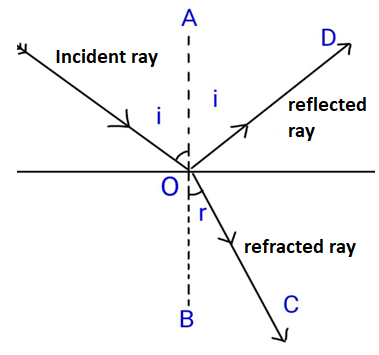
The angle between reflected and refracted ray is $\angle COD=180-(i+r)=90$
So, the answer is 90°.

Additional information:
There is a law named after scientist Brewster about polarization of light by reflection. It says that, at the polarizing angle, $\tan\theta=\mu$ . Where $\mu$ is the refractive index of the reflecting medium.

Note: Don’t confuse this polarization with the polarization of a Dielectric. These are two different phenomena. Note that light is polarized when the incidence angle has a particular value. Also know that the refracted ray is not polarized here.