Question

At moderate pressure, the compressibility factor for gas is given as: $Z{\text{ }} = {\text{ }}1{\text{ }} + {\text{ }}0.35{\text{ }}P - \dfrac{{168}}{T}{\text{ }}P$, where P is in bar and T is in Kelvin. What is Boyle's temperature of the gas?
A. $168{\text{ }}K$
B. $480{\text{ }}K$
C. $58.8{\text{ }}K$
D. $575{\text{ }}K$

Answer 1

The gases which follow the gas laws at every condition and temperature are called an ideal gas. To solve this question the given formula will be used. at a moderate temperature, the value of Z will be 1. Then after rearranging the equation the value of Boyle’s temperature can be calculated.

Complete step by step answer:
The compressibility factor (Z) is the thermodynamic property to modifying the ideal gas law to account for the behavior of real gas.
Boyle’s temperature is the temperature at which real gases obey the gas law at a wide range of pressure.
Now at a moderate temperature, the value of the compressibility factor (Z) is 1.
Therefore, put the value in the given equation and find out the boyle’s temperature is,

$$Z{\text{ }} = {\text{ }}1{\text{ }} + {\text{ }}0.35{\text{ }}P - \dfrac{{168}}{T}{\text{ }}P \\\ 1 = {\text{ }}1{\text{ }} + {\text{ }}0.35{\text{ }}P - \dfrac{{168}}{T}{\text{ }}P \\\ 1 - 1 = {\text{ }}0.35{\text{ }}P - \dfrac{{168}}{T}{\text{ }}P \\\ 0 - 0.35{\text{ }}P = {\text{ }} - \dfrac{{168}}{T}{\text{ }}P \\\ 0.35{\text{ }} = {\text{ }}\dfrac{{168}}{T}{\text{ }} \\\ {\text{ T}} = {\text{ }}\dfrac{{168}}{{0.35}}{\text{ }} \\\ {\text{T = 480K}} \\\$$

Therefore, Boyle's temperature is 480K.

So, the correct option is B.

Note:
The diagram between the compressibility factor of different gases versus pressure.

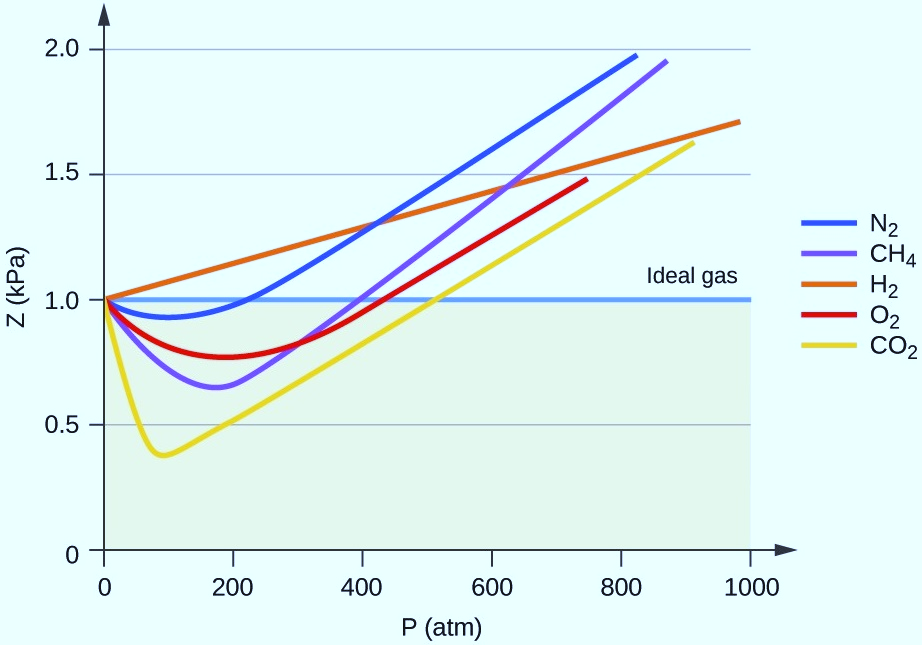
In this diagram, it is clear that at low pressure(up to 500atm) carbon dioxide shows the most ideal behavior than other gases. Hydrogen has the most deviation from ideal behavior events at low pressure.