Question

At Boyle's temperature, the graph of Z v/s P is drawn for $H_2$. Select incorrect graph(s):

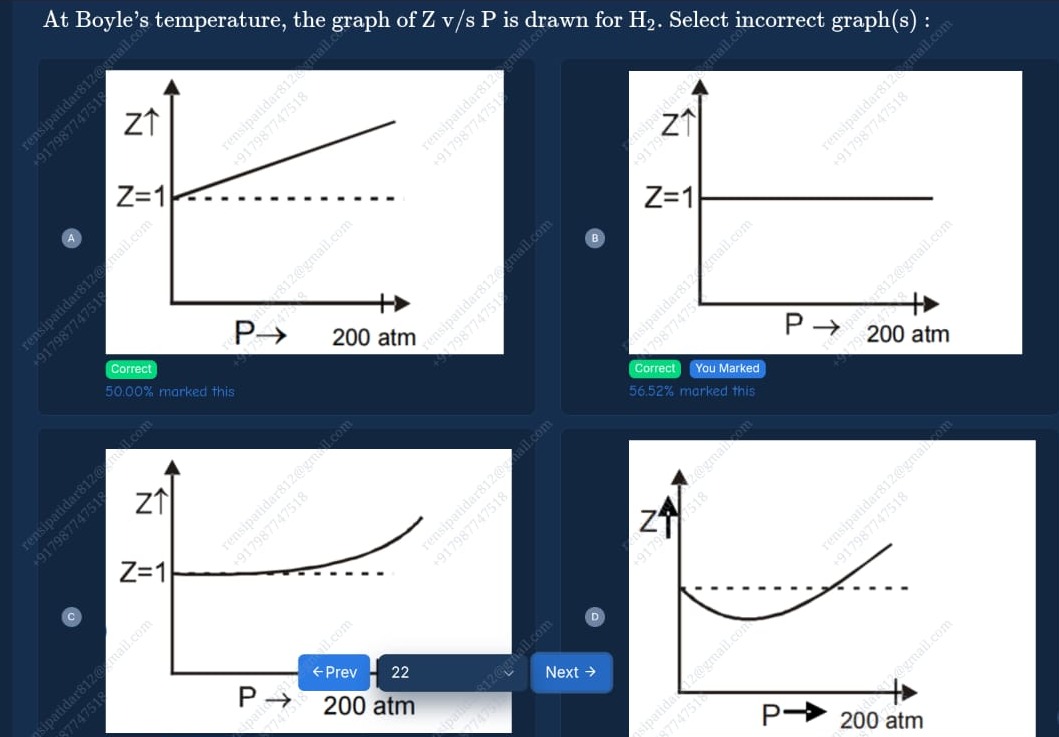
• A. Graph A: Z starts at 1 and increases linearly with P.
• B. Graph B: Z is constant at 1 for all pressures.
• C. Graph C: Z starts at 1 at P=0 and increases with pressure. The curve is concave up
• D. Graph D: Z starts at 1 at P=0, initially decreases below 1, reaches a minimum, and then increases.

Answer 1

Answer: (C)

A, B, D

Answer 2

The compressibility factor $Z$ is defined as $Z = \frac{PV}{nRT}$. For a real gas, the virial equation of state can be written as $Z = 1 + B_2(T)P + C_2(T)P^2 + \dots$.

Boyle's temperature ($T_B$) is the temperature at which the second virial coefficient $B_2(T_B) = 0$.

At Boyle's temperature, the virial equation becomes $Z = 1 + C_2(T_B)P^2 + D_2(T_B)P^3 + \dots$

For most gases, the third virial coefficient $C_2(T)$ is positive. For $H_2$, $C_2(T_B) > 0$.

Therefore, at Boyle's temperature and low pressures, $Z \approx 1 + C_2(T_B)P^2$. Since $C_2(T_B) > 0$, $Z$ starts at 1 at $P=0$ and increases with pressure. The initial slope $\frac{dZ}{dP}$ at $P=0$ is zero, since $\frac{dZ}{dP} = 2C_2(T_B)P + \dots$, which is 0 at $P=0$. The curve of Z vs P is initially concave up as the second derivative $\frac{d^2Z}{dP^2} = 2C_2(T_B) + \dots$ is positive at low pressure.

Let's analyze the given graphs:

• Graph A: Z starts at 1 and increases linearly with P. This would imply $Z = 1 + kP$ with $k>0$. The initial slope is constant and positive, which contradicts the behavior at Boyle's temperature where the initial slope is zero. So, Graph A is incorrect.

• Graph B: Z is constant at 1 for all pressures. This represents an ideal gas, not a real gas like $H_2$ at Boyle's temperature over a range of pressures. While $B_2(T_B)=0$, higher order terms are non-zero, so Z deviates from 1 as pressure increases. So, Graph B is incorrect.

• Graph C: Z starts at 1 at P=0 and increases with pressure. The curve is concave up, consistent with $Z \approx 1 + CP^2$ at low pressures where $C>0$. This graph correctly represents the behavior of $H_2$ at its Boyle's temperature.

• Graph D: Z starts at 1 at P=0, initially decreases below 1, reaches a minimum, and then increases. This behavior occurs at temperatures below the Boyle temperature, where attractive forces dominate at low pressures, leading to $Z < 1$. At Boyle's temperature, $Z$ is always greater than or equal to 1 (at P=0, Z=1; at P>0, Z>1). So, Graph D is incorrect.

The question asks to select the incorrect graph(s). Based on our analysis, graphs A, B, and D are incorrect.