Question

At any instant, a wave travelling along the string is shown in the figure below. Here, if A is a point moving upwards, then which of the following statements is true?

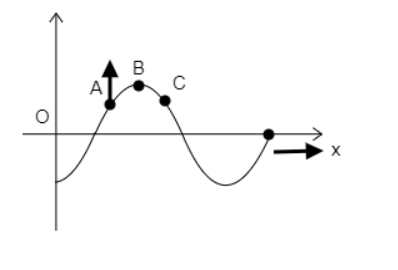
A) The wave is travelling to the right.
B) The displacement amplitude of the wave is equal to the displacement of B at this instant.
C) At this instant, C is also directed upwards.
D) Statements 1 and 3 are true.

Answer 1

The direction of motion of a point in the wave is given by its instantaneous velocity at that point which depends on the slope of the wave at that point and the velocity of the wave. If the velocity of the wave is positive then the wave must be travelling to the right and if it is negative it travels to the left. The displacement amplitude refers to the maximum displacement in the y-direction.

Formula used:
The instantaneous velocity of a particle in a wave is given by, ${v_p} = - v\left( {\dfrac{{dy}}{{dx}}} \right)$ where, $v$ is the velocity of the wave and $\dfrac{{dy}}{{dx}}$ is the slope of the wave at that particular point in the wave.

Complete step by step answer:
Step 1: Sketch the direction of the velocity of the wave at the different points in the wave using relation for the instantaneous particle velocity of a wave.
Consider the point A in the wave. It is mentioned that A is moving upwards. This suggests the instantaneous velocity of the particle at A is positive. Also, we observe the slope of the wave $\dfrac{{dy}}{{dx}}$ at A is positive.
The instantaneous velocity of a particle at A in a wave is given by, ${v_p} = - v{\left( {\dfrac{{dy}}{{dx}}} \right)_A}$ ------- (1)
where $v$ is the velocity of the wave and $\dfrac{{dy}}{{dx}}$ is the slope of the wave at A in the wave.
Substituting only the signs of the instantaneous velocity and slope at A in equation (1) we obtain $\left( + \right) = - \left( v \right) \times \left( + \right)$
For the signs on both sides of the above equation to match $v$ must be negative. This implies that the wave is travelling to the left.
So option A is incorrect.
Now using equation (1) we can also find the instantaneous velocity at C.
At C, the slope of the wave is negative. We have established that the velocity of the wave is negative. So by substituting the signs of $v$ and ${\left( {\dfrac{{dy}}{{dx}}} \right)_C}$in equation (1) we get, $\left( {{v_p}} \right) = - \left( - \right) \times \left( - \right) = - {v_p}$
i.e., the instantaneous velocity at C is negative which implies that C is moving downwards.
So the option C is incorrect.

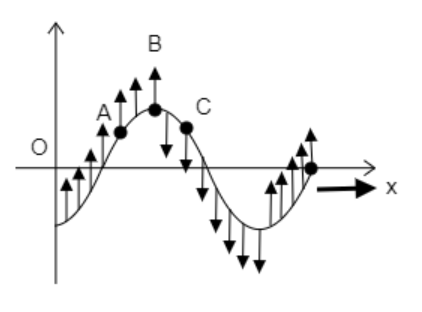
So we obtain the directions of each point in the wave as in the figure given below. From the above figure, we notice that B is at the peak of the wave. So, the displacement at B will be the maximum displacement and so it can be referred to as the displacement amplitude of the wave.

Thus the option B is correct.

Note:
The slope at A in the wave is positive because the points before and after A are such that the wave builds up to its peak which suggests that the slope is increasing. However, at C, the wave decreases to its negative peak. So the slope is negative at C.