Question: At an instant the point P in the figure represents the instantaneous center of rotation for a unifor...

Question

At an instant the point P in the figure represents the instantaneous center of rotation for a uniform rectangular plate ABCD $\left( {12cm \times 10cm} \right)$ At the given instant the point A (Corner) has velocity $24cm/sec)$ The magnitude of the velocity of the center of mass of the plate is:

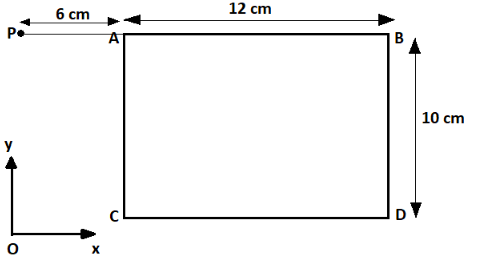
A. $13cm/s$
B. $26cm/s$
C. $52cm/s$
D. $104cm/s$

Answer 1

Solution

In order to solve this you have to know the concept of center of mass. Also remember that the center of mass of the rectangular plate will always lie at its center. The center of mass is a position defined relative to an object or system of objects.

Complete step by step solution:
Here, in this question take a point M at the center of the rectangular plate shown in the figure below
And then draw a perpendicular NM on the side AB and also join point P with the center point M as shown in the figure below

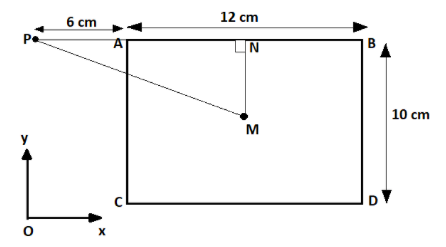
As we know that the M is the center point. So the point N on the side AB is the midpoint of that side.
Hence, $NM = 5cm$ and $AN = 6cm$
As we know that the center of mass of the rectangular plate ABCD will lie at its center.
Using pythagoras theorem, we get
$P{M^2} = M{N^2} + N{P^2}$
On putting the values, we get
$P{M^2} = {5^2} + {\left( {6 + 6} \right)^2}$
On further solving, we get
$PM = \sqrt {25 + 144} = 13cm$
Now, the angular velocity of point A is given by,
$\omega = \dfrac{v}{{PA}}$
Here $v$ is the velocity of point A which is given in the question as $v = 24cm/s$
On putting the values in the above equation, we have
$\Rightarrow \omega = \dfrac{{24}}{6} = 4cm/s$
All the points in the plate will rotate with this same angular velocity. Therefore, the velocity of center of mass M is given by
${v_M} = PM \times \omega$
On putting the value we have
$\Rightarrow {v_M} = 13 \times 4 = 52cm/s$
Hence, the magnitude of the velocity of the center of mass of the plate is $52cm/s$

Therefore, the correct option is C

Note: Always keep in mind that as long as the system is closed, the velocity of center of mass of the system doesn’t change. The system moves as if all the mass is concentrated at a single point. The main characteristics of the center of mass of any system is that it appears to carry the whole mass of the system.