Question

At an instance of time O is a point on the string at which its displacement is zero. At the same instant a point, P which is at a distance $\dfrac{\lambda }{8}$ from O, has the displacement A. The displacement of a point at a distance $\dfrac{\lambda }{4}$ from O is $\dfrac{{nA}}{{\sqrt 2 }}$, calculate the value of n?

Answer 1

The shape of the wave (at any fixed instant) as a function of time x is a sine wave. This question can be solved using the wave equation formula. Wavelength $\lambda$ is the distance between two consecutive crests or troughs. At point ‘O’, since its displacement is zero, its amplitude is zero; we can consider it as the origin point in the diagram.

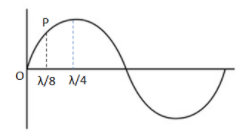
Complete step-by-step solution:
At a fixed time t, displacement y varies as a function of position x. That is $y = A'\sin (kx)$, where k= $\dfrac{{2\pi }}{\lambda }$
So from the equation $y = A'\sin (kx)$
Substituting the value of k we get, $y = A'\sin (\dfrac{{2\pi }}{\lambda }x)$
For point P which is at a distance $\dfrac{\lambda }{8}$ from O, has the displacement A, the wave equation becomes
$A = A'\sin (\dfrac{{2\pi }}{\lambda }*\dfrac{\lambda }{8})$ , displacement$y = A$; distance $x =$ $\dfrac{\lambda }{8}$
Simplifying we get, $A = A'\sin (\dfrac{\pi }{4})$
Since $\sin (\dfrac{\pi }{4}) = \dfrac{1}{\sqrt 2}$ We get, $A = A'*\dfrac{1}{{\sqrt 2 }}$
Therefore by rearranging we get, $A' = \sqrt 2 A$………..(1)
For the point at a distance $\dfrac{\lambda }{4}$ from O with displacement $\dfrac{{nA}}{{\sqrt 2 }}$, the wave equation becomes
$y = A'\sin (\dfrac{{2\pi }}{\lambda }x)$
Substituting y = $$$\dfrac{{nA}}{{\sqrt 2 }}$; x = $$$\dfrac{\lambda }{4}$The wave equation becomes,$\dfrac{{nA}}{{\sqrt 2 }} = A'\sin (\dfrac{{2\pi }}{\lambda }*\dfrac{\lambda }{4})$Simplifying we get,$\dfrac{{nA}}{{\sqrt 2 }} = A'\sin (\dfrac{\pi }{2})$Since$\sin (\dfrac{\pi }{2}) = 1$, wave equation becomes$\dfrac{{nA}}{{\sqrt 2 }} = A'$From equation (1) we know that$A' = \sqrt 2 A$Substituting for A’ in the above equation$\dfrac{{nA}}{{\sqrt 2 }} = A'$, gives$\dfrac{{nA}}{{\sqrt 2 }} = \sqrt 2 A$Cross multiplying and cancelling similar terms we get,$nA = (\sqrt 2 *\sqrt 2 )A = 2A$$n = 2$

Note: Wave is a form of disturbance that travels through a medium as a result of the periodic motion of the particles in the medium. Waves not only transport energy but its pattern of disturbance contains information that propagates from one point to another. There are mainly three types of waves: mechanical, electromagnetic and matter waves.