Solveeit Logo
Login

Question

Question: At an extreme of a function \( f\left( x \right) \) , the tangent to the curve is (a) Parallel to...

At an extreme of a function f(x)f\left( x \right) , the tangent to the curve is
(a) Parallel to the x – axis.
(b) Perpendicular to the x – axis
(c) Inclined at an angle of 45° to the x – axis
(d) Inclined at an angle of 60° to the x – axis

Explanation

Solution

Hint : We will solve this method with two methods. First, we will draw a random curve f(x)f\left( x \right) which moves with increase in the value of x and has one extreme. Then, we will draw a tangent at the extreme and observe its orientation. Then, we will solve it analytically to get the value of slope and with the value of slope, we can find the orientation of the tangent.

Complete step-by-step answer :
First, we will graph the function f(x)=x2−2f\left( x \right)={{x}^{2}}-2 . We know that the graph of the function x2{{x}^{2}} has one extreme.

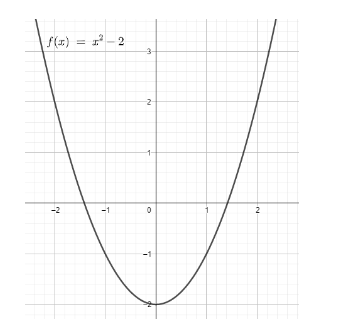
Now, we will draw a tangent to the curve at the extreme, which we can observe is at (0, ─2).

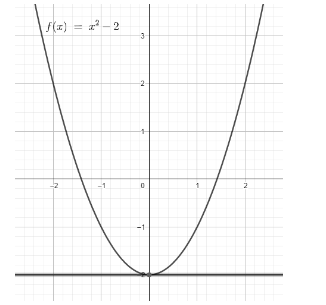
As we can see, the tangent is parallel to the x – axis.
Now, mathematically, to find the extreme to curve, we find the first derivative of the curve and equate it to zero.
Also, to find the tangent at curve at a given point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) on the curve, we find the first derivative of the curve at (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) .
Let us again consider the function f(x)=x2−2f\left( x \right)={{x}^{2}}-2 .
The first derivative of the function will be df(x)dx=d(x2−2)dx\dfrac{df\left( x \right)}{dx}=\dfrac{d\left( {{x}^{2}}-2 \right)}{dx}
⇒f′(x)=2x\Rightarrow f'\left( x \right)=2x
To find the extreme, put f′(x)=0f'\left( x \right)=0
⇒0=2x ⇒x=0 \begin{aligned} & \Rightarrow 0=2x \\\ & \Rightarrow x=0 \\\ \end{aligned}
Now, put x = 0 in the function f(x)=x2−2f\left( x \right)={{x}^{2}}-2
⇒f(0)=(0)2−2 ⇒f(0)=−2 \begin{aligned} & \Rightarrow f\left( 0 \right)={{\left( 0 \right)}^{2}}-2 \\\ & \Rightarrow f\left( 0 \right)=-2 \\\ \end{aligned}
Therefore, the extreme is at (0, ─2).
Now, substitute (0, ─2) in f′(x)=2xf'\left( x \right)=2x to find the slope at the extreme (0, ─2)
⇒f′(0)=0\Rightarrow f'\left( 0 \right)=0
Therefore, the slope at the tangent of the curve at the extreme (0, ─2) is 0.
Thus, we can say that the tangent is parallel to the x – axis.
Thus, option (a) is the correct option.

Note : Students can opt any of the above methods to show that the tangent at the extreme of the function f(x)f\left( x \right) is parallel to the x – axis. Whenever the slope is 0, the line is parallel to the x – axis.