Question

At a given place where the acceleration due to gravity is $g{\text{ m}}{{\text{s}}^{ - 2}}$ , a sphere of lead od density $d{\text{ kg}}{{\text{m}}^{ - 3}}$ is gently released in a column of liquid of density $\rho {\text{ kg}}{{\text{m}}^{ - 3}}$ . If $d > \rho$ the sphere will
A) Fall vertically with an acceleration $g{\text{ m}}{{\text{s}}^{ - 2}}$.
B) Fall vertically with no acceleration.
C) Fall vertically with an acceleration $g\left( {\dfrac{{d - \rho }}{d}} \right)$ .
D) Fall vertically with an acceleration $g\left( {\dfrac{\rho }{d}} \right)$ .

Answer 1

When the sphere is released in the liquid column, the force due to gravity will be directed downwards and the force of buoyancy (or upthrust) will be directed upwards. So the magnitude of the net force acting on the sphere will be the difference in magnitude of the force due to gravity and the upthrust. The acceleration of the sphere can then be obtained from the net force.

Formulas used:
The mass of an object is given by, $m = Vd$ where $V$ is the volume of the object and $d$ is its density.
The force due to gravity is given by, ${F_g} = mg$ where $m$ is the mass of the body and $g$ is the acceleration due to t gravity.
The force of buoyancy is given by, ${F_b} = V\rho g$ where $V$ is the volume of the liquid displaced, $\rho$ is the density of the liquid and $g$ is the acceleration due to t gravity.

Complete step by step answer:
A lead sphere is gently dropped in a liquid column. A buoyant force will be acting on the sphere in a direction opposite to the force due to gravity. We have to determine the acceleration of the sphere as it moves down the column. A figure of the mentioned problem is given below.

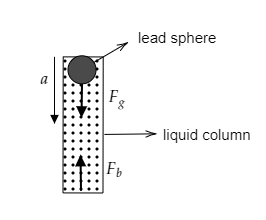
The density of the lead sphere is $d{\text{ kg}}{{\text{m}}^{ - 3}}$ and the density of the liquid is $\rho {\text{ kg}}{{\text{m}}^{ - 3}}$.
Let $V$ be the volume of the sphere and that of the displaced liquid.
Then the mass of the sphere will be $m = Vd$.
Let $a$ be the acceleration of the lead sphere inside the column.
The forces acting on the lead sphere inside the liquid column are the force due to gravity and the force of buoyancy. Both have opposite directions.
Thus the net force is given by, ${F_{net}} = ma = {F_g} - {F_b}$ ------- (1)
The force due to gravity is given by,
$\Rightarrow {F_g} = mg = Vdg$ and the force of buoyancy is given by, ${F_b} = V\rho g$ .
Substituting these expressions of force in equation (1) we get,
$ma = Vdg - V\rho g$
$\Rightarrow a = \dfrac{{Vg\left( {d - \rho } \right)}}{m}$
Substituting for $m = Vd$ in the above relation and simplifying we get,
$a = \dfrac{{Vg\left( {d - \rho } \right)}}{{Vd}} = \dfrac{{g\left( {d - \rho } \right)}}{d}$

Thus the sphere will fall with an acceleration of $a = \dfrac{{g\left( {d - \rho } \right)}}{d}{\text{ m}}{{\text{s}}^{ - 2}}$. So the correct option is C.

Note:
Alternate method:
As the sphere falls through the column, its weight feels to reduce due to the upthrust of the liquid.
Then the apparent weight of the sphere is given by,
${W_{app}} = {W_s} - {\text{upthrust}}$ ; ${W_s}$ is the weight of the sphere.
We have ${W_{app}} = ma = Vda$ , ${W_s} = mg = Vdg$ and ${\text{upthrust}} = V\rho g$ .
$\Rightarrow Vda = Vdg - V\rho g$
Cancelling out the similar terms we get,
$da = \left( {d - \rho } \right)g$ or $a = \dfrac{{\left( {d - \rho } \right)g}}{d}$
Thus the sphere will fall with an acceleration $a = \dfrac{{\left( {d - \rho } \right)g}}{d}{\text{ m}}{{\text{s}}^{ - 2}}$ .