Question

At a curved path of the road, the road bed is raised a little on the side away from the center of the curved path. The slope of the road bed is given by
A. $\tan \theta = \dfrac{{rg}}{{{v^2}}}$
B. $\tan \theta = \dfrac{{rg}}{{{v^2}}}$
C. $\tan \theta = \dfrac{{{v^2}}}{{rg}}$
D. $\tan \theta = \dfrac{{{v^2}g}}{r}$

Answer 1

In this question, first assume that the road is inclined with an angle $\theta$and then we will resolve the angles for an object moving on the inclined road in the horizontal and the vertical direction and then solving both the equation to find the slope of the road bed.

Complete step by step answer:
Let the angle through which road bed is raised be $\theta$.Mass of an object on the bed be $m$. Velocity of the object through which it is moving be $v$.

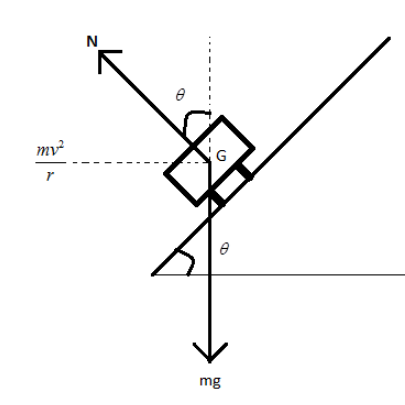
From the above diagram we can see the road is inclined with an angle $\theta$so the normal acting on the object will also incline with an angle $\theta$.Now if we resolve the normal with an angle $\theta$in horizontal and the vertical direction we can write,
In x-direction $N\operatorname{Sin} \theta$
In y-direction $N\operatorname{Cos} \theta$
Hence by applying Newton's law in horizontal and the vertical directions we can write,
$N\sin \theta = \dfrac{{m{v^2}}}{r} - - (i)$
$N\cos \theta = mg - - (ii)$
Now divide equation (i) by equation (ii), hence we get

$$\dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}} \\\ \Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{\dfrac{{{v^2}}}{r}}}{g} \\\ \therefore\tan \theta = \dfrac{{{v^2}}}{{rg}} \\\$$

Hence the slope of the road bed will be $\tan \theta = \dfrac{{{v^2}}}{{rg}}$

Hence,option C is correct.

Note: Slope plays a vital role in making the vehicles turn on the curved road. If the road is curved without any slope (slope 0) then, the chance of accidents increases. Students must note that to make the turning of a vehicle safe on a curved road the outer edge of the road is raised above the inner edge to make some inclination with the horizontal.