Question

At a certain height, a shell at rest explodes into two equal fragments. One of the fragments receives a horizontal velocity u. The time interval after which the velocity vectors will be inclined at ${{120}^{\circ }}$ to each other is
$\begin{aligned} & a)\dfrac{u}{\sqrt{3}g} \\\ & b)\dfrac{\sqrt{3}u}{g} \\\ & c)\dfrac{2u}{\sqrt{3}g} \\\ & d)\dfrac{u}{2\sqrt{3}g} \\\ \end{aligned}$

Answer 1

The shells explode at a particular height from the ground. Both of them have the same mass as a result by law of conservation of momentum; both will travel with the same initial horizontal velocity. Hence we can use Newton’s first kinematic equation to write the velocity of the fragments at time t and express them in vector form. Then we can use the dot product of the two vectors to find time t when the fragments are ${{120}^{\circ }}$ with respect to each other.

Complete step by step answer:
To begin with let us draw the diagram to visualize the scenario.

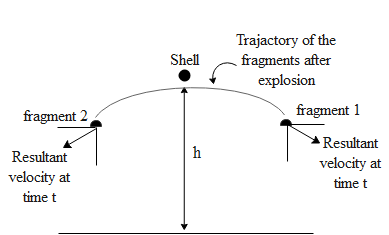
In the above figure we can clearly see that the shell let us say of mass M, explodes into two fragments and moves in a particular path downwards due to gravity. The initial momentum of the particle is zero. Also it is given in the question that the fragments have equal mass (m) and one of the fragments(1) receives a horizontal velocity u. Therefore by law of conservation of momentum along the horizontal we get,
$\text{MV = mu+mv, }$
Where V is the initial velocity of the shell and ‘v’ is the velocity of the other fragment. Since initial velocity i.e. V=0, therefore
$\begin{aligned} & \text{M}\left( \text{0} \right)\text{=mu+mv} \\\ & \Rightarrow u=-v \\\ \end{aligned}$
Therefore we can conclude that both the fragments will have the same velocity horizontal velocity but move in opposite directions. The resultant vector of the velocities of both the fragments will have horizontal components and the vertical component that changes with time. The vertical components of velocities of the both the fragments with respect to time t using Newton’s first kinematic equation we get,
$V(\text{fragment 1})=U+a\text{t and }V(\text{fragment 2})=U+a\text{t }$, where U is the initial velocity along the vertical. When the shell explodes there is no component of velocity along the vertical. Therefore,
$\begin{aligned} & V(\text{fragment 1})=a\text{t }and \\\ & V(\text{fragment 2})=a\text{t} \\\ \end{aligned}$
Both the above particles are accelerating due to gravity. Therefore the above equations can be written as,
$\begin{aligned} & V(\text{fragment 1})=g\text{t }and \\\ & V(\text{fragment 2})=g\text{t} \\\ \end{aligned}$
Now let us write the velocities of each of the fragments in vector form. Let $\overset{\wedge }{\mathop{i}}\,$ be the unit vector along the horizontal and $\overset{\wedge }{\mathop{j}}\,$ be the unit vector along the vertical. Therefore the velocities of each fragment in vector form is,
$\begin{aligned} & V(\text{fragment 1})=u\overset{\wedge }{\mathop{i}}\,+g\text{t}\overset{\wedge }{\mathop{j}}\,\text{ }and \\\ & V(\text{fragment 2})=-u\overset{\wedge }{\mathop{i}}\,+g\text{t}\overset{\wedge }{\mathop{j}}\, \\\ \end{aligned}$
The angle between any two vectors using the dot product can be given as,
$\operatorname{Cos}\theta =\dfrac{\overrightarrow{A}.\overrightarrow{B}}{magnitude of \overrightarrow{A}\times magnitude of \overrightarrow{B}}$, where $\text{ }\\!\\!\theta\\!\\!\text{ }$ is the angle between vectors $\overrightarrow{\text{A }}\text{and }\overrightarrow{\text{B}}.$
Substituting the velocity vectors of both the fragments in the adjacent equation we get,
$\begin{aligned} & \operatorname{Cos}\theta =\dfrac{(u\overset{\wedge }{\mathop{i}}\,+g\text{t}\overset{\wedge }{\mathop{j}}\,).(-u\overset{\wedge }{\mathop{i}}\,+g\text{t}\overset{\wedge }{\mathop{j}}\,)}{\sqrt{{{u}^{2}}+{{\left( gt \right)}^{2}}}\sqrt{{{u}^{2}}+{{\left( gt \right)}^{2}}}}\text{, }\theta \text{=12}{{\text{0}}^{\text{o}}} \\\ & \Rightarrow -\dfrac{1}{2}=\dfrac{-{{u}^{2}}+{{\left( gt \right)}^{2}}.}{{{\left( \sqrt{{{u}^{2}}+{{\left( gt \right)}^{2}}} \right)}^{2}}} \\\ & \Rightarrow \dfrac{-{{u}^{2}}-{{\left( gt \right)}^{2}}}{2}=-{{u}^{2}}+{{\left( gt \right)}^{2}} \\\ & \Rightarrow \dfrac{-{{u}^{2}}}{2}+{{u}^{2}}={{\left( gt \right)}^{2}}+\dfrac{{{\left( gt \right)}^{2}}}{2} \\\ & \Rightarrow \dfrac{{{u}^{2}}}{2}=\dfrac{3}{2}{{\left( gt \right)}^{2}} \\\ & \Rightarrow \dfrac{{{u}^{2}}}{3{{g}^{2}}}={{t}^{2}} \\\ & \Rightarrow t=\dfrac{u}{\sqrt{3}g} \\\ \end{aligned}$
Hence the correct answer to the above question is option a.

Note:
It is to be noted that there is no component of velocity along the vertical during the explosion. Hence we have taken the initial component of vertical velocity to be zero in Newton's first kinematic equation. Therefore both the fragments will be along the same horizontal line and at the same distance from the vertical line i.e. h in the figure. Hence both the fragments will make an angle 60 degrees during time $t=\dfrac{u}{\sqrt{3}g}$.