Question

At a certain height a body at rest explodes into two equal fragments with one fragment receiving a horizontal velocity of $10m{{s}^{-1}}$. The time interval after the explosion for which the velocity vectors of the two fragments become perpendicular to each other is $\left( g=10m{{s}^{-2}} \right)$
A. $1 s$
B. $2 s$
C. $1.5 s$
D. $1.75 s$

Answer 1

First find the velocity of the other fragment by the law of conservation momentum. Both the fragments will accelerate under the force of gravity. Thus find the velocity vectors of both the fragments with kinematic equations. The dot product of the two velocities when they are perpendicular to each other is zero.

Complete step by step answer:
The body explodes into two fragments due to the internal forces. Let us assume that there is no external force acting on the system and the resultant of the internal forces of a system is always zero. This means the net force on the system is zero. Hence, the momentum of the system is conserved. This means that the momentum of the system before explosion is equal to the momentum of the system after explosion.Momentum of a body moving velocity v is given as $\overrightarrow{P}=m\overrightarrow{v}$.
Since the body is at rest before explosion, its momentum is zero. This means that the net momentum of the two fragments (of equal mass) is zero.

It is given that one fragment travels in the horizontal direction (say in the positive x-axis direction) with a speed of $10m{{s}^{-1}}$.Therefore, the other fragment must travel in the direction of the negative x-axis with the same speed of $10m{{s}^{-1}}$so that the net momentum of the system is zero. This means that just after the explosion both the fragments are travelling along the horizontal with velocities $10\widehat{i}m{{s}^{-1}}$ and $-10\widehat{i}m{{s}^{-1}}$ (as shown).

Now, both the fragments will undergo projectile motion under the gravity force. Since the gravitational force acts in the downwards direction, the fragment will accelerate in the downwards direction with an acceleration of g. This means that the only velocity in the vertical direction will change with time and the velocity along the horizontal will remain constant.Let us now use the kinematic equation $\overrightarrow{v}=\overrightarrow{u}+\overrightarrow{a}t$ for the vertical motion of both the fragments. Here, $\overrightarrow{u}$ is the initial velocity of the particle, $\overrightarrow{a}$ is its acceleration and $\overrightarrow{v}$ is the velocity at time t.
In this case, $\overrightarrow{u}=0$, $\overrightarrow{a}=-g\widehat{j}=-10\widehat{j}\left( m{{s}^{-2}} \right)$.

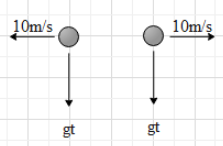
Therefore, the vertical velocity of each fragment at time t is $\overrightarrow{v}=-(10t)\widehat{j}$.
Therefore, the velocities of the fragments at time t are $\overrightarrow{{{v}_{1}}}=10\widehat{i}-10t\widehat{j}$ and $\overrightarrow{{{v}_{2}}}=-10\widehat{i}-10t\widehat{j}$.

When the velocities of the two fragments are perpendicular to each other, the dot product of the two vectors will be zero.
i.e. $\overrightarrow{{{v}_{1}}}.\overrightarrow{{{v}_{2}}}=0$
$\Rightarrow \overrightarrow{{{v}_{1}}}.\overrightarrow{{{v}_{2}}}=\left( 10\widehat{i}-10t\widehat{j} \right).\left( -10\widehat{i}-10t\widehat{j} \right)=0$
$\Rightarrow (10)(-10t)+(-10)(-10t)=0$
$\Rightarrow -100+100{{t}^{2}}=0$
$\Rightarrow {{t}^{2}}=1$
$\therefore t=1s$
Therefore, the time interval after the explosion for which the velocity vectors of the two fragments become perpendicular to each other is 1 s.

Hence, the correct option is A.

Note: There is one more way by which we can find the time after which the velocities of the two fragments are perpendicular to each other. If we imagine the given situation, then we will find that the motion of the system is symmetric about the vertical axis. Therefore, when the angle between the two velocities is 90 degrees, each one will be making an angle of 45 degrees with the vertical. Now, we can analyse the motion of the single fragment and find the time after which its velocity makes an angle of 45 degrees with the vertical by using the appropriate kinematic equations.