Question
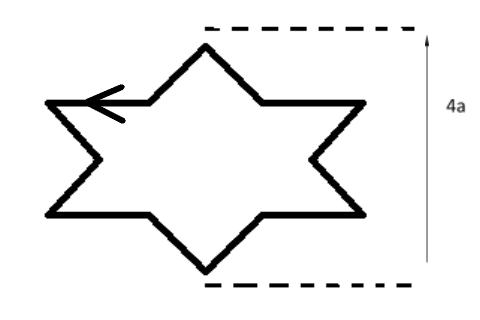
Question: Asymmetric star shaped conducting wire loop is carrying a steady state current I as shown in the fig...
Asymmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the centre of the loop is :
a. 4πaμ0I6[3−1]
b. 4πaμ0I3[3−1]
c. 4πaμ0I6[3+1]
d. 4πaμ0I3[2−3]
Solution
Magnetic field due to current carrying conductor (here the conductor is given in the star shape in the question) is given by Ampere’s circuital law. In mathematical terms it is given as:
4πaμ0I(sinϕ1+sinϕ2)
Here, I is the current flowing in the conductor,
a is the distance of magnetic field from the conductor and
ϕ1 and ϕ2 are the angles which are observed in the figure.
Complete step by step answer:
Ampere’s circuital law states that: line integral of magnetic field surrounding a closed loop equals the number of times the algebraic sum of currents passing through the loop.
Now come to the calculation part:
Value of angles in which we observe in the figure given in the question is:
600 and 300
One triangle of the star is making 600 but in order to find the magnetic field due to the current carrying on the outer side of the triangle we will subtract angle 300 from the total angle.
Our expression will become as:
⇒4πaμ0I(sin600−sin300) ⇒4πaμ0I(23−21) (We have substituted the values of both the angles) -----(1)
As the current loop has 12 sides we have calculated the magnetic field due to one side, so we will multiply the expression 1 by 12.
⇒4πaμ0I×212[3−1] ⇒4πaμ0I6[3−1] (We have taken 21 common and 12 is divided by 2).
Hence, the correct answer is option (A).
Note: Ampere circuital has a very well known application which is that the concept of Ampere’s circuital law is used by current carrying solenoid, for because of which magnetic induction is observed. Phenomenon of magnetic induction is used in transformers for linking the windings.
