Question

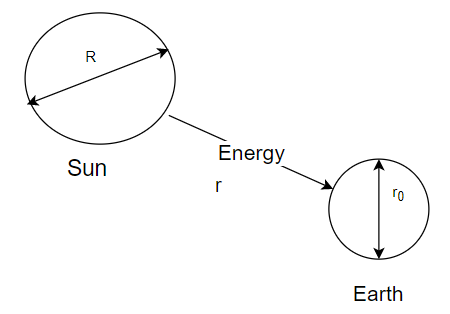
Assuming the sun to be a spherical body of radius $R$ at a temperature of $T\,K$. Evaluate the intensity of radiant power, incident on Earth, at a distance $r$ from the sun where ${r_0}$ is the radius of the earth and $\sigma$ is Stefan’s constant:
(A) $\dfrac{{{R^2}\sigma {T^4}}}{{{r^2}}}$
(B) $\dfrac{{4{\pi ^2}{R^2}\sigma {T^4}}}{{{r^2}}}$
(C) $\dfrac{{{\pi ^2}{R^2}\sigma {T^4}}}{{{r^2}}}$
(D) $\dfrac{{{\pi ^2}{R^2}\sigma {T^4}}}{{4\pi {r^2}}}$

Answer 1

Sun is assumed to be a black body which continuously emits energy. Hence use Stefan’s formula to calculate the energy emitted by the sun per second. With the help of that answer, find the energy received by the earth by substituting the given or assumed details.

Formulae Used:
(1) By the Stefan’s law of black body,
$P = \sigma A{T^4}$
Where P is the energy of radiant power emitted by the sun per second, $A$ is the total area of the sun, $\sigma$ is the stefan- Boltzmann constant which is equal to $1.714 \times {10^{ - 9}}$ and $T$ is the temperature of the sun.
(2) Area of the circle
$A = 4\pi {R^2}$
Where $R$ is the radius of the sun.
(3) Energy received by the earth
${P_E} = Ia$
Where ${P_E}$ is the energy received by the earth, $I$ is the intensity of the energy received by the earth and $a$ is the area of the Earth.

Complete step-by-step solution:
The assumed data from the question are
Sun is assumed to be a spherical body of the radius, $R$
Distance between the sun and the earth, $r$
Radius of the earth, ${r_0}$
Assuming the sun as the spherical black body, Stefan’s law is applicable to it.

$P = \sigma A{T^4}$
Substituting the formula for area in the above equation
$P = 4\sigma \pi {R^2}{T^4}$………………(1)
Since the sun is far away from the Earth, $r \gg {r_0}$
Intensity of the sun at the Earth is obtained by dividing the total intensity emitted by the sun per second by the area to which it emits.
$I = \dfrac{P}{A}$
Substituting the equation (1) in the above equation.
$I = \dfrac{{4\sigma \pi {R^2}{T^2}}}{{4\pi {r^2}}}$
By simplifying the above equation.
$I = \dfrac{{\sigma {R^2}{T^2}}}{{{r^2}}}$………………………(2)
To calculate the total radiant power emitted by the sun to the earth surface,
${P_E} = Ia$
Substituting (2) in the above formula. Assuming the Earth to be a round body, hence its area is $\pi {r^2}$
${P_E} = \dfrac{{\sigma {R^2}{T^2} \times \pi r_0^2}}{{{r^2}}}$
Thus the option (B) is correct.

Note:- Remember that the sun is assumed to be spherical so its area is taken as $4\pi {R^2}$ and Earth is assumed to be in disc shaped and hence its area is taken as $\pi r_0^2$. Care must be taken in simplifying and substituting the formulae given.