Question

Assuming covalent radii to be additive property; The benzene ring is regular hexagon and each ${\text{C}} - {\text{I}}$ bond lies on a line passing through the center of hexagon. The ${\text{C}} - {\text{C}}$ bond length in ${{\text{C}}_{\text{6}}}{{\text{H}}_{\text{6}}}$ is ${\text{1}}{\text{.40}}\mathop {\text{A}}\limits_{}^{\text{o}}$ and covalent radius of iodine and carbon atom are $1.33\mathop {\text{A}}\limits_{}^{\text{o}}$ and $0.77\mathop {\text{A}}\limits_{}^{\text{o}}$ . Also neglect different overlapping effects. The sum of iodine- iodine distances in o-, m-, p- di iodobenzene is ${\text{X}}\mathop {\text{A}}\limits_{}^{\text{o}}$ . Value of $100{\text{X}}$ is:

Answer 1

To answer this question, you must recall the structures and angles of the hexagonal structure of benzene. Each angle in a regular hexagon has an angle of ${120^{\text{o}}}{\text{C}}$ and lengths of all the sides are equal.

Complete step by step solution:
First we consider the ortho- di- iodobenzene molecule.

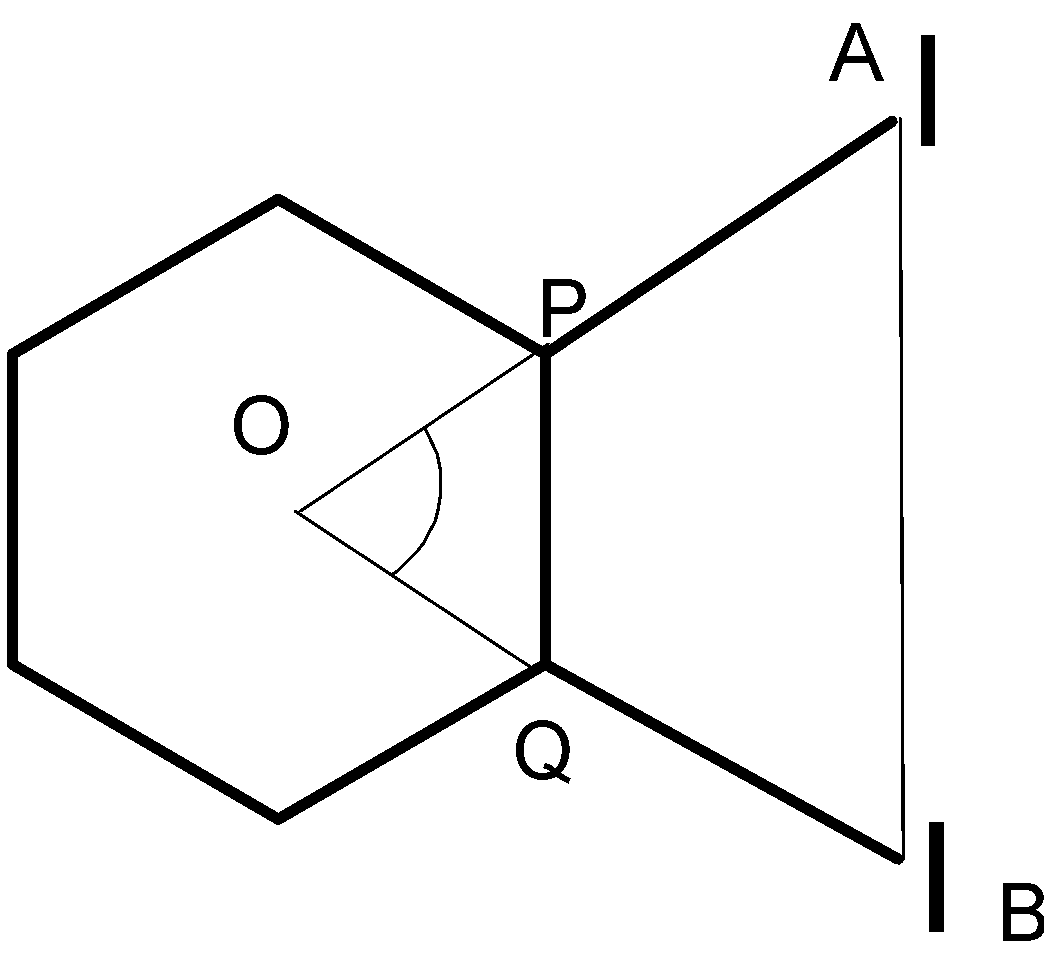
We are given that the carbon- iodine bond lies on the line passing through the center of the hexagon. Such a line also bisects the carbon- carbon bond angle thus, the angle becomes ${60^{\text{o}}}$ . We know that both the carbon iodine bonds are identical, thus, the distance from the center of the hexagon to the iodine atoms will be equal.
Thus, OA = OB and the angle is ${60^{\text{o}}}$ . So, the triangle OAB is an equilateral triangle. In an equilateral triangle, all the sides are equal. So we can write $AB = OA = OB$
Similarly the triangle OPQ is also equilateral. So, $OP = OQ = PQ = 1.40{\text{ }}\mathop {\text{A}}\limits^0$
We are supposed to find the distance between two iodine atoms, i.e. AB
$AB = OA = OP + PA$
$AB = 1.40 + 1.33 + 0.77$
So, the distance between iodine atoms in ortho- di- iodobenzene is ${\text{AB}} = {\text{3}}{\text{.50}}\mathop {\text{A}}\limits^{\text{o}}$
Now in meta- di- iodobenzene molecule,

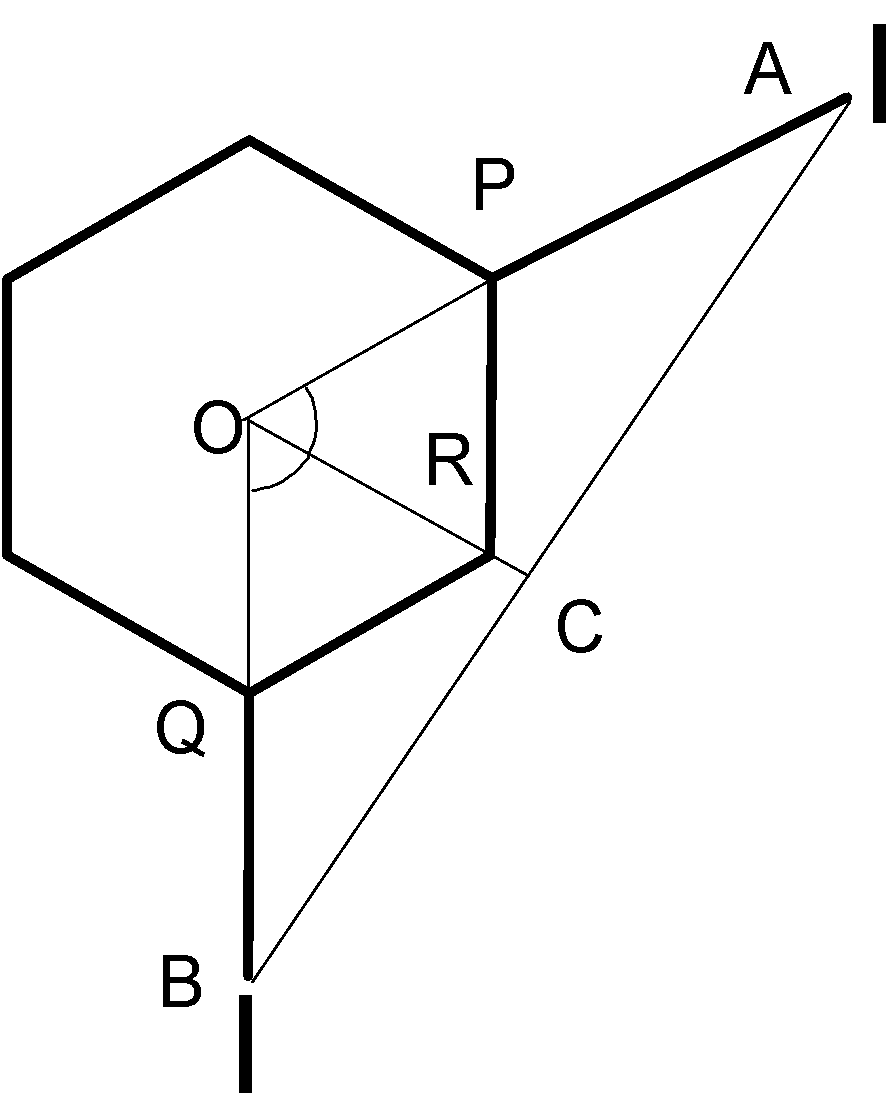
The angle formed at the center of the hexagon will be equal to ${60^{\text{o}}} + {60^{\text{o}}} = {120^{\text{o}}}$ . Since we know from earlier calculations that OA must be equal to OQ, thus the angle A and angle B will be equal to ${30^{\text{o}}}$ in the triangle OAB. The two triangles OAC and OBC are congruent since all sides are of equal lengths. We are supposed to find AB which is given by,
$AB = AC + BC = 2AC$
Substituting:
$\Rightarrow AB = 2AO\cos 30 = 2\left( {3.50} \right)\cos 30$
Solving:
$\Rightarrow AB = 6.06\mathop {\text{A}}\limits^{\text{o}}$
In Para- di- iodobenzene molecule,

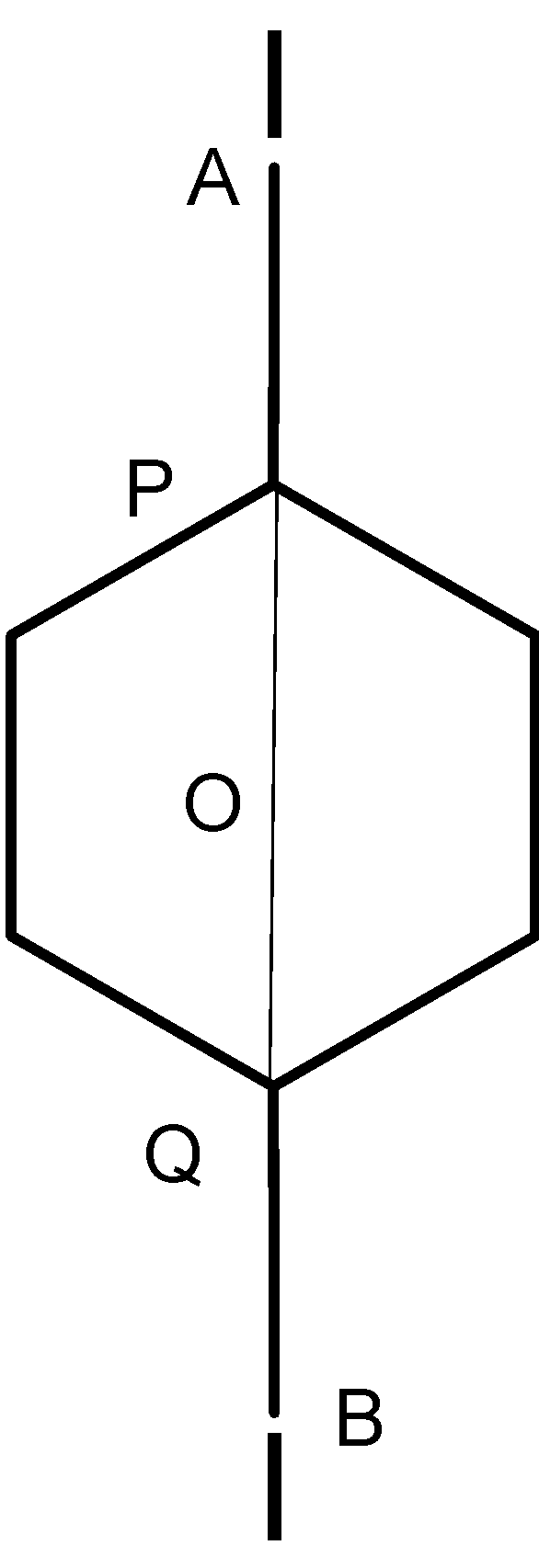
$AB = OA + OB$
$\Rightarrow AB = OP + OQ + PA + BQ$
Substituting:
$\Rightarrow AB = 1.40 + 1.40 + 1.33 + 0.77 + 1.33 + 0.77$
Solving:
$\therefore AB = 7.0\mathop {\text{A}}\limits^{\text{o}}$
The sum of all three values of AB gives us X. So, $X = 3.50 + 6.06 + 7$
$X = 16.56\mathop {\text{A}}\limits^{\text{o}}$
$100X = 1656$ .

Note:
In an equilateral triangle, the angles at the bases of equal sides are equal. In an equilateral triangle, all the sides and angles are equal. Since the sum of all angles in the triangle is 180 degrees, each angle in an equilateral triangle is equal to 60 degrees.