Question

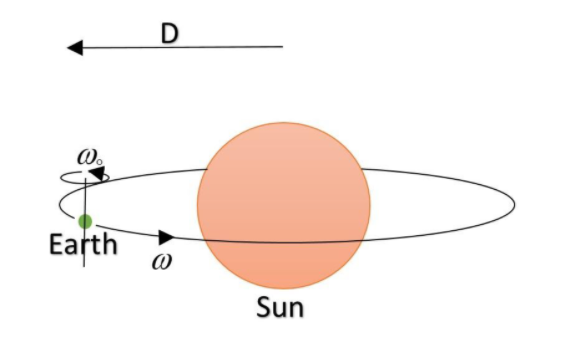
Assume the earth’s orbit around the sun as circular and the distance between their centres as ‘D’. Mass of the earth is ‘M’ and its radius is ‘R’. If the earth has an angular velocity ‘$\omega_\circ$’ with respect to its centre and ‘$\omega$’ with respect to the centre of the sun. The total kinetic energy of the earth is:
$\text{A.}\quad \dfrac{MR^2\omega_\circ^2}{5}\left( 1 + \left[\dfrac{\omega}{\omega_\circ}\right]^2 + \dfrac 52 \left[\dfrac{D\omega}{R\omega_\circ}\right]^2\right)$
$\text{B.}\quad \dfrac{MR^2\omega_\circ}{5}\left( 1 + \dfrac 52 \left[\dfrac{D\omega}{R\omega_\circ}\right]^2\right)$
$\text{C.}\quad \dfrac 25 MR^2\omega_\circ^2\left( 1 + \left[\dfrac{\omega}{\omega_\circ}\right]^2 + \dfrac 52 \left[\dfrac{D\omega}{R\omega_\circ}\right]^2\right)$
$\text{D.}\quad \dfrac 25 MR^2\omega_\circ^2\left( 1 + \dfrac 52 \left[\dfrac{D\omega}{R\omega_\circ}\right]^2\right)$

Answer 1

Every planet has its own rotation as well as revolution. By rotation we mean the angular movement of the planet about its own axis. By revolution, we mean the angular movement of the planet around the axis of sun. As we have some energy associated with each rotation, hence the total energy of the planet is the sum total of energies due to both types of rotations.

Formula used:
Rotational Kinetic energy = $\dfrac 12 I\omega^2$and parallel axis theorem: $I_{axis} = I_{C.O.M} + Md^2$

Complete answer:
As the earth has two types of angular movements, hence there are also two types of rotational kinetic energies. The energy associated with the rotation of earth about it axis is given by:
$K.E._{earth} = \dfrac 12 \dfrac25 MR^2 \omega_\circ^2 = \dfrac 15 MR^2\omega_\circ^2$
[As moment of inertia of a sphere about its centre of mass = $\dfrac 25 MR^2$]
Also $K.E._{about\ sun} = \dfrac 12 I_s\omega^2$
Now, for $I_s$, we must use parallel axis theorem, given by:
$I_s=I_{C.O.M}+MD^2$
$I_s=\dfrac 25 MR^2+MD^2$
Now, putting it in the equation:
$K.E._{about\ sun} = \dfrac 12 \left( {\dfrac 25 MR^2+MD^2} \right)\omega^2 = \left( \dfrac 15 MR^2 + \dfrac 12 MD^2\right)\omega^2$
Now, the total energy of earth is $K.E._{About\ earth} + K.E. _{About\ sun} =\dfrac 15 MR^2 \omega_\circ^2 + \left( \dfrac 15 MR^2 + \dfrac 12 MD^2\right)\omega^2$
Taking $\dfrac{MR^2\omega_\circ ^2}{5}$common from total kinetic energy, we get:
$K.E_{total} = \dfrac{MR^2\omega_\circ ^2}{5}\left[ 1\left(1 + \dfrac{\omega^2}{\omega_\circ ^2}\right) + \dfrac 52 \dfrac{D^2}{R^2} \dfrac{\omega^2}{\omega_\circ^2} \right]$
Or $K.E_{total} = \dfrac{MR^2\omega_\circ^2}{5}\left( 1 + \left[\dfrac{\omega}{\omega_\circ}\right]^2 + \dfrac 52 \left[\dfrac{D\omega}{R\omega_\circ}\right]^2\right)$

Hence, option A. is correct.

Note:
One must not get confused about the moment of inertia being $mr^2$ about any axis. Note that this is a moment of inertia in case of a point mass only. But in case of an object having definite mass and volume, we have to use the parallel axis theorem. There’s no other way to avoid this. Hence the chance of mistake is high here and one should avoid it. Also, parallel axis theorem is valid for all bodies, constraint being that the two axis must be parallel to each other. But in-case of a perpendicular axis theorem, the body must be planar. It is not applicable for 3d objects.