Question
Question: Assume that two liquids in a U-shape tube are water and oil. Compute the density of oil if water sta...
Assume that two liquids in a U-shape tube are water and oil. Compute the density of oil if water stands 19cm above the interface and oil stands 24cm above the interface.
Solution
Pressure of a fluid at any point will be the same throughout its volume if we neglect its weight. But the weight of a fluid is not negligible so it varies according to depth of a point. The more is the depth, the more will be the pressure at that layer of fluid. The pressure at the same level of the liquid is constant at any point on that level irrespective of the shape of the container.
Formula used:
P=P0+hρg
Where, P is the pressure at depth h of the fluid
P0 is the pressure at the surface of the fluid (atmospheric pressure)
h is the depth of the liquid
ρ is the density of the liquid
g is acceleration due to gravity
Complete step by step answer:
Let’s consider a point A at a depth of h from the surface of the fluid. The pressure exerted at any point of the same depth is represented by the formula
P=P0+hρg
We are given the question that, water stands 19cm above the interface and oil stands 24cm above the interface.
Let’s look at the following diagram.
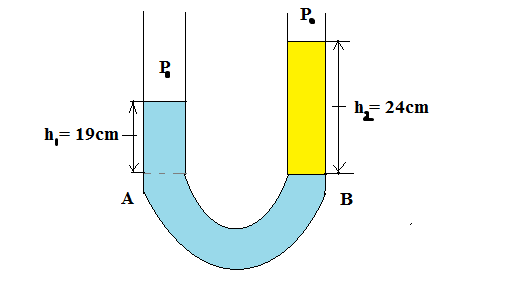
From the above figure, as points A and B are on the same level, pressure is the same at both the points.
Thus we can write, PA=PB ……………………. (1)
Where, PA is the pressure at point A and PB is the pressure at point B.
Point A is at a depth h1=19cm from the surface and point B is at a depth of h2=24cm from the surface.
Let’s consider the densities of water and oil as ρ1 and ρ2 respectively.
Now substituting the corresponding values of variables in the pressure-depth formula, we get,
For water, at point A,
PA=P0+h1ρ1g ………. (2)
For oil, at point B,
PB=P0+h1ρ1g ………. (3)
From equation (1),
PA=PB
Putting the values of PA and PB in this equation we get,
⇒P0+h1ρ1g=P0+h2ρ2g
Cancelling P0 from both sides, we get,
⇒h1ρ1g=h2ρ2g
Dividing by g in both sides we get,
⇒h1ρ1=h2ρ2 ……….. (4)
The density of water in C.G.S units is 1gcm−3
Now substituting the values of h1, ρ1 and h2 in equation (4), we get,
⇒19×1=24×ρ2
⇒ρ2=2419=0.791gcm−3
Thus the density of oil in C.G.S units is 0.791gcm−3.
Notes: Water is taken as a universal measure of relative density of a fluid. The density of water at 4∘C is 1gcm−3 in C.G.S units and 1000kgm−3 in S.I units. Interface means the level where the fluids meet, which in this case is point B. the formula used is the pressure-depth formula because pressure is not constant throughout the fluid, but it is different at different depths.
