Question

Assertion: There is a triangular plate as shown. A dotted axis is lying in the plane of slab. As the axis is moved downwards, the moment of inertia of the slab will first decrease then increase.
Reason: Axis is first moving towards its centre of mass and then it is receding from it.

A) If both assertion and reason are true and the reason is the correct explanation of the assertion.
B) If both assertion and reason are true but reason is not the correct explanation of assertion.
C) If the assertion is true and the reason is false.
D) If the assertion is false but the reason is true.

Answer 1

The parallel axis theorem can be used to solve this problem and find the correct answer for this problem. The parallel axis theorem is used when the moment of inertia about the centre of mass is given and we need to calculate the moment of inertia to be calculated which is at an axis parallel to the axis passing through the centre of mass and which is at some distance d.

Formula: The parallel axis theorem is $I' = {I_{cm}} + m \cdot {d^2}$ if ${I_{cm}}$is the moment of inertia of center of mass, $I'$ is the moment of inertia about axis which is parallel to the${I_{cm}}$ and $m$ is the mass also $d$ is the distance between the two parallel axes.

Step by step solution:
Let ${I_{cm}}$ be the moment of inertia of triangular plate about centre of mass and ${I'}$ be the moment of inertia about the axis which is as shown in the figure also $m$ be the mass and $d$ be the distance between ${I'}$ and ${I_{cm}}$.

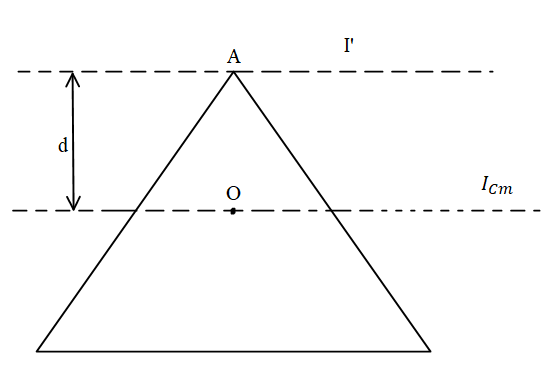
According to the parallel axis theorem the $I'$ will vary as the distance between the $I'$ and ${I_{cm}}$ will vary since $I' = {I_{cm}} + m \cdot {d^2}$ if the axis from point A will move towards point O then their will be decrease in the distance between $I'$ and ${I_{cm}}$ therefore $I'$ decreases first but after it passes the point O the distance starts increasing causing to increase the $I'$.Therefore the moment of inertia first decreases and then decreases.

So the correct answer for this problem is option A because the assertion and reason both are correct and the reason is the correct explanation for the assertion.

Note: The condition for applying the parallel axis theorem is that the two axes should be parallel and one of the axes should pass through the centre of mass also the distance between the two axes should be known. Students should remember how to apply the parallel axis theorem because sometimes while solving any problem a student may need to find the moment of inertia about another axis which is parallel to a given axis and is at some distance away.