Question
Question: Assertion: The maximum refractive index of liquid for total internal reflection of the ray passing t...
Assertion: The maximum refractive index of liquid for total internal reflection of the ray passing through the prism as shown in figure must be 2.
Reason: Here, critical angle is 45∘.
(A) Both assertion and reason are true but the reason is the correct explanation of assertion.
(B) Both assertion and reason are true but the reason is not the correct explanation of assertion.
(C) Assertion is true but reason is false.
(D) Both assertion and reason are false.
(E) Reason is true but the assertion is false.
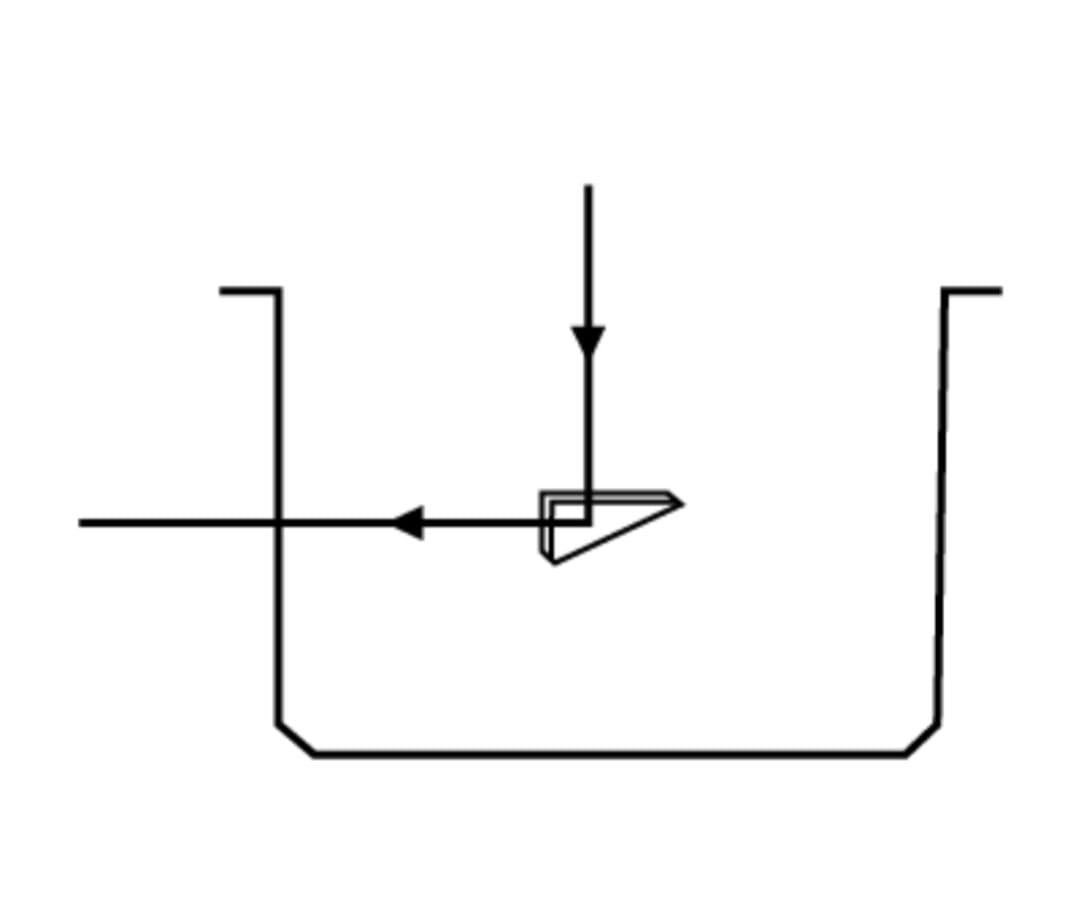
Solution
We will use the formula for critical angle, i.e., sinC=μ11=μ1μ2. refractive index of the first medium with respect to the second medium; μ1= refractive index of denser medium and μ2= refractive index of rarer medium.
Complete step by step answer:
We know the formula for finding the critical angle is sinC=μ11=μ1μ2 …………………. (i)
The value of the refractive index of the liquid w.r.t the prism is given as 2.
sinC=21 (on substituting the value of 2μ1 in Eq., (i)
⇒C=sin−1(21)
⇒C=45∘
This means that both assertion and reason are true and the reason is the correct explanation for assertion.
Hence, option (a.) is the correct answer.
Note: The assertion and reason both hold true only for the given values of refractive index and critical angle. So, we will always have to calculate and check the answer.
