Question

Assertion: In circular motion work done by all the forces acting on the body is zero.
Reason: Centripetal force and velocity are mutually perpendicular.
A. Both Assertion and Reason are correct, and Reason is the correct explanation for Assertion.
B. Both Assertion and Reason are correct, but Reason is not the correct explanation for Assertion.
C. The Assertion is correct, but Reason is incorrect.
D. Both Assertion and Reason are incorrect.

Answer 1

-The given problem is of circular motion. You need to cross-check the two statements here by applying the concepts of circular motion along with the work done formula.

Complete step by step answer:
Circular motion is described by the motion of the body in a path which is circular or in some part it shows circular motion tendency. The circular motion has a centripetal force which is acting towards its centre, and it is mainly responsible for this type of motion.
The velocity of the body is along the circle, i.e., it is tangential to the circular path. As we can see it, the figure ${F_c}$ is the centripetal force, and v is the tangential velocity.

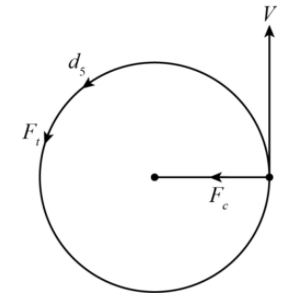
When the body is moving in uniform velocity, then there is no acceleration, and in this case, there is no work done.
The centripetal force is always perpendicular to the velocity as shown in the figure, so the displacement is also perpendicular to the centripetal force
Then according to the work done formula $W = Fds\cos \theta$.
The work done is $W = {F_c} \times ds\cos {90^0} = 0$
In the case of tangential force, the displacement and the force is always in the same direction so $\theta = 0$ . Thus there is work done.
Because, When the body is moving with nonuniform velocity, then there is acceleration In the tangential direction also so there will be a tangential force.
${F_t} = m{a_t}$ , Where${a_t}$ is the tangential acceleration and m is the mass of the body.
Now for calculating the work done, we will use the work done formula $W = Fds\cos \theta$ . In the case of tangential force, the displacement and the force is always in the same direction so $\theta = 0$ . Thus there is work done.

So, the correct answer is “Option D”.

Note:
You can go wrong here in understanding the centripetal and tangential force.
Because when the velocity is nonuniform, then two types of acceleration come into existence.