Question

As the position of an object reflected in a concave shell mirror of focal length $0.25{\text{ }}m$ is varied, the position of the image varies. Plot the image distance as a function of the object distance, letting the latter change from $0$ to $\infty$. Where is the image real and where is it virtual?

Answer 1

We have to make use of the mirror formula and substitute the value of focal length. Then, by putting different values of object distance $u$, as the image distance $v$ is a function of $u$. By putting different values and analysing them we will eventually plot the graph and find the position of it being real and imaginary.

Complete step by step answer:
Let the image distance be $v$ and the object distance be $u$. The given question has provided focal length as $0.25{\text{ }}m$.
The mirror formula is given as-
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Now when $u = f$ we get, $v = \infty$.
Again when, $u = \infty$ we get, $v = f$.
Again, when we take, $u < f$ then $v$ is a $- ve$ quantity.
Again, when $u > f$ then $v$ is a $+ ve$ quantity.
Now, when $u = 0$, we get,
$v = \dfrac{{uf}}{{u + f}} = \dfrac{{0 \times f}}{{0 + f}} = 0$ thus $v = 0$.
Now we can eventually plot the graph. It will be a curve line as it decreases and also increases after a certain point.
We have to only plot the graph considering $u$ from $0$ to $\infty$ as per the question.

The graph is thus, being plotted below:

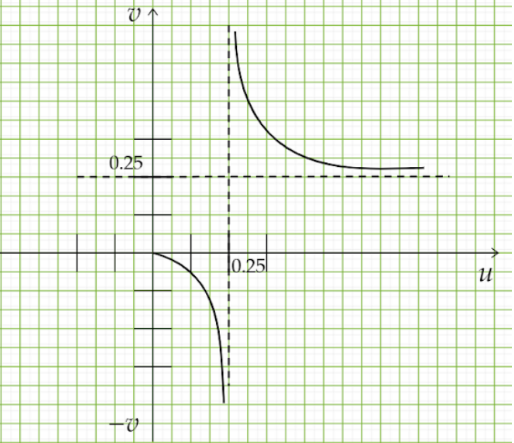
The image is virtual from $0$ to $\simeq f$ and real from $\simeq f$ to $\infty$.

Note: It must be noted that according to the mirror for when the image or object is at the left side of the pole or downward of the principal axis of the mirror then it is considered to be of $- ve$ sign and hence called a real image. When the image or object is at the right side of the pole or upward of the principal axis of the mirror then it is considered to be of $+ ve$ sign and hence called a virtual image.