Question

As shown in the given figure the ball is given sufficient velocity at the lowest point to complete the circle. Length of the string is 1m. Find the tension in the string, when it is at ${{60}^{\circ }}$ with vertical position. (mass of ball is 5kg)

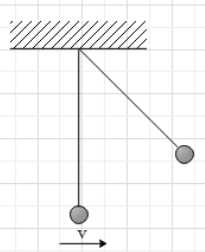
A. 160N
B. 180 N
C. 200 N
D. 225 N

Answer 1

Use the condition for the minimum velocity that has to be given to a simple pendulum at the lowest point, to complete one complete one full circular path and find the initial velocity of the ball. Then use the work energy theorem to find its speed at an angle of ${{60}^{\circ }}$. Analyse the net force along the string and find the tension.

Formula used:
$W=mgh$
where W is work done by gravity force when a body of mass m falls by height h and g is acceleration due to gravity.
$K=\dfrac{1}{2}m{{v}^{2}}$
where K is kinetic energy of the body moving speed v.
${{a}_{c}}=\dfrac{{{v}^{2}}}{l}$
where ${{a}_{c}}$ is centripetal acceleration rotating with speed v in a circular path of radius l.

Complete step by step answer:
The minimum velocity that has to be given to a simple pendulum at the lowest point, to complete one complete one full circular path is given to be $v=\sqrt{5gl}$, g is acceleration due to gravity and l is the length of the pendulum.
The given system of the ball and the string can be considered as a simple pendulum.
Therefore, the value of v is equal to $v=\sqrt{5gl}$.
It is given that $l=1m$ and the value of $g=10m{{s}^{-2}}$.
Then,
$v=\sqrt{5gl}=\sqrt{5(10)(1)}=\sqrt{50}m{{s}^{-1}}$.
Let us first find the speed of the ball, when it is at an angle of ${{60}^{\circ }}$ with vertical position. This can be done using the work energy theorem, which says that total work done on a system is equal to change in its kinetic energy.
i.e. $W=\Delta K$

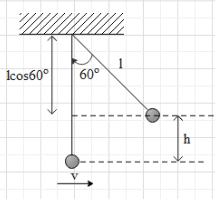
From the figure we get that $h=l-l\cos {{60}^{\circ }}$.
$h=1-(1)\dfrac{1}{2}=\dfrac{1}{2}m$
Therefore, work done by gravitational force is $W=-mgh=-(5)(10)\left( \dfrac{1}{2} \right)=-25J$.
(the work done by gravity is negative because the direction of the force and the displacement of the block are opposite).
The initial kinetic energy of the system is ${{K}_{1}}=\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}(5){{\left( \sqrt{50} \right)}^{2}}=125J$
The final velocity of the block is ${{v}_{2}}$. Therefore, is final kinetic energy is ${{K}_{2}}=\dfrac{1}{2}(5)v_{2}^{2}=\dfrac{5}{2}v_{2}^{2}$
Hence, $\Delta K=\dfrac{5}{2}v_{2}^{2}-125$ …. (ii)
Now, equate (i) and (ii).
$-25=\dfrac{5}{2}v_{2}^{2}-125$
$\Rightarrow v_{2}^{2}=\dfrac{100\times 2}{5}=40$

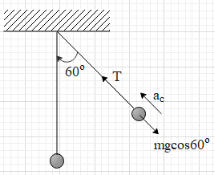
At this position, the net force on the ball, along the string is $F=T-mg\cos {{60}^{\circ }}$.
The ball will have some centripetal acceleration ${{a}_{c}}=\dfrac{v_{2}^{2}}{l}$
And we know that $F=m{{a}_{c}}$
Then,
$T-mg\cos {{60}^{\circ }}=m{{a}_{c}}$
Which means that $T-mg\cos {{60}^{\circ }}=m\dfrac{v_{2}^{2}}{l}$
Now, substitute all the known values in the above equation.
$\Rightarrow T-(5)(10)\left( \dfrac{1}{2} \right)=(5)\left( \dfrac{40}{1} \right)$
$\therefore T=25+200=225N$
Therefore, the tension in the string is 225N.

Hence, the correct option is D.

Note: If you do not know about the work energy theorem, then you can also use the law of conservation of mechanical energy since gravitational force is a conservative force.The law of conservation of mechanical energy says that the change in kinetic energy is equal to the negative of the change in potential energy of the system.