Solveeit Logo
Login

Question

Question: As shown in the figure water squirts horizontally out of two small holes in the side of the cylinder...

As shown in the figure water squirts horizontally out of two small holes in the side of the cylinder and the two streams strike the ground at the same point. If hole Q is at height ‘h’ above ground and level of water stands to a height H, then the height of p above the ground level is.

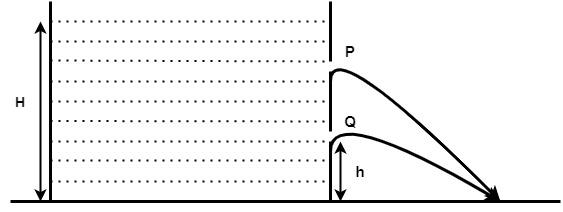
A) 2h
B) H/h
C) (H-h)
D) None

Explanation

Solution

Here we have to apply the concept of conservation of energy. The net external energy applied to the system is conserved. So, by this relation the potential energy and the kinetic energy of the system is equal and also the range of squirting water of the two holes are at the same place (Range is equal). Apply the formula of kinematics and conservation of energy (P.E + K.E) and solve.

Complete step by step solution:
Apply conservation of energy
mgh2=12mv12mg{h_2} = \dfrac{1}{2}m{v_1}^2 ;
The mass are same so it will cancel out each other,
gh2=12v12g{h_2} = \dfrac{1}{2}{v_1}^2;
Simplify the above equation
gh2×2=v12g{h_2} \times 2 = {v_1}^2;
v1=2gh2{v_1} = {\sqrt {2gh} _2};
For hole P
mg(H−h)=12mv22mg(H - h) = \dfrac{1}{2}m{v_2}^2;
g(H−h)=12v22g(H - h) = \dfrac{1}{2}{v_2}^2;
2g(H−h)=v222g(H - h) = {v_2}^2;
v2=2g(H−h){v_2} = \sqrt {2g(H - h)} ;

Step 2:
Find out the time taken to reach the surface at the same place for both the holes.
Apply equations of kinematics:
S=ut+12at2S = ut + \dfrac{1}{2}a{t^2} ;
No initial vertical velocity:
S=12gt2S = \dfrac{1}{2}g{t^2};
For hole P, assume the distance to beh2{h_2}.
(H−h2)=12gt12(H - {h_2}) = \dfrac{1}{2}g{t_1}^2;
2(H−h2)=gt122(H - {h_2}) = g{t_1}^2;
2(H−h2)g=t12\dfrac{{2(H - {h_2})}}{g} = {t_1}^2;
t1=2(H−h2)g{t_1} = \sqrt {\dfrac{{2(H - {h_2})}}{g}} ;
For hole Q,
S=ut+12at2S = ut + \dfrac{1}{2}a{t^2};
Here also the initial velocity is zero:
S=12gt22S = \dfrac{1}{2}g{t_2}^2;
h=12gt22h = \dfrac{1}{2}g{t_2}^2;
2hg=t22\dfrac{{2h}}{g} = {t_2}^2;
t2=2hg{t_2} = \sqrt {\dfrac{{2h}}{g}} ;
Step 3: Here the range of the holes are the same R1=R2{R_1} = {R_2}
R=vt+12at2R = vt + \dfrac{1}{2}a{t^2}.
Here there is no horizontal acceleration so a = 0.
The equation becomes
R=vtR = vt;
R1=R2{R_1} = {R_2};
v1t1=v2t2{v_1}{t_1} = {v_2}{t_2};
Put the values in the above equation:
2gh2×2(H−h2)g=2g(H−h)×2hg\sqrt {2g{h_2}} \times \sqrt {\dfrac{{2(H - {h_2})}}{g}} = \sqrt {2g(H - h)} \times \sqrt {\dfrac{{2h}}{g}} ;
Solve the above equation:
2gh2×2(H−h2)g=2g(H−h)×2hg2g{h_2} \times \dfrac{{2(H - {h_2})}}{g} = 2g(H - h) \times \dfrac{{2h}}{g};
Simplify
2h2×2(H−h2)=2(H−h)×2h2{h_2} \times 2(H - {h_2}) = 2(H - h) \times 2h;
Simplify it further,
⇒h2×(H−h2)=(H−h)×h\Rightarrow {h_2} \times (H - {h_2}) = (H - h) \times h;
⇒(Hh2−h22)=(Hh−h2)\Rightarrow (H{h_2} - {h_2}^2) = (Hh - {h^2});
⇒(Hh2−h22−Hh+h2)=0\Rightarrow (H{h_2} - {h_2}^2 - Hh + {h^2}) = 0;
⇒(Hh2−Hh)+(−h2+h22)=0\Rightarrow (H{h_2} - Hh) + ( - {h^2} + {h_2}^2) = 0;
⇒H(h2−h)+(−h2+h22)=0\Rightarrow H({h_2} - h) + ( - {h^2} + {h_2}^2) = 0;
Solving the above equation we get,
⇒h2=(H−h)\Rightarrow {h_2} = (H - h)

Option (C) is correct. The height of p above the ground level is (H−h)(H - h).

Note: Here we have to find out the velocity as well as time taken and then equate the two values together as the distance i.e. the range of the two holes squirting the water is equal. After equating there would be a relation of height H and h.