Question
Question: As shown in the figure, water squirts horizontally out of two small holes in the side of the cylinde...
As shown in the figure, water squirts horizontally out of two small holes in the side of the cylinder and the two streams strike the ground at the same point. If the hole Q is at a height h above the ground and the level of water stands at height H above the ground, then the height of P above ground level is
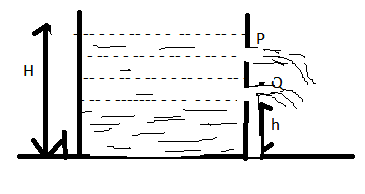
Solution
In order to solve this question, we need to calculate the equations of the point Q and P differently. For this we will use Bernoulli's Equation,
p+21ρV2+ρgh=constant, where pis the pressure, Vis the velocity, his the elevation and gis the gravitational acceleration. There are different equations for different types of cases.
From the figure,
For the point Q,
x=2(H−h)h
For the point P,
x=2h′(H−h′)
Where x=horizontal range of water.
Thereafter,
2(H−h)h=2h′(H−h′)
=(H−h)h=h′(H−h′)
Or h′2−h′H+h(H−h)=0
Now, after solving it, we get
h′=(H−h)
Additional Information: According to Bernoulli’s equation, if we follow a small volume of fluid along its path, various quantities in the sum may change, but the total remains constant. Bernoulli’s equation is, in fact, just a convenient statement of conservation of energy for an incompressible fluid in the absence of friction. Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy, potential energy and internal energy remains constant
Note: While solving this question, it should be kept in mind that it is an application of Bernoulli’s equation. Bernoulli’s equation deals with the flow of fluid. We should apply Bernoulli's equation to solve the question as it is asked to.
