Question
Question: As shown in the figure, two infinitely long, identical wires are bent by \({90^ \circ }\) and placed...
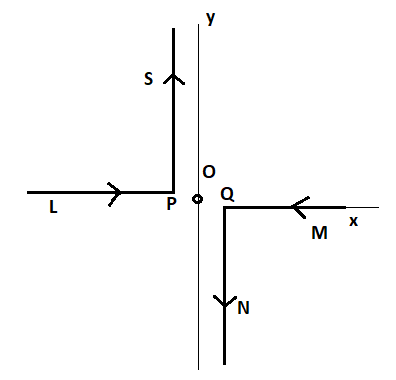
As shown in the figure, two infinitely long, identical wires are bent by 90∘ and placed in such a way that the segments LP and QM are along the x-axis, while segments PS and QN are parallel to the y-axis, if OP=OQ=4cm, and the magnitude of the magnetic field at O is 10−4T, and the two wires carry equal currents (see figure), the magnitude of the current wire and the direction of the magnetic field at O will be (μ0=4π10−7NA−2)
A) 40A, Perpendicular into the page
B) 40A, perpendicular out of the page
C) 20A, perpendicular out of the page
D) 20A, perpendicular into the page
Solution
Recall the formula for the magnetic field due to a straight wire. Always remember that whenever there are two segments along the same axis and the direction of current is opposite to each other then the magnetic field due to these segments is zero. Here only find the magnetic field due to the segment PS and QN.
Formula used:
Magnetic field due to a straight wire,
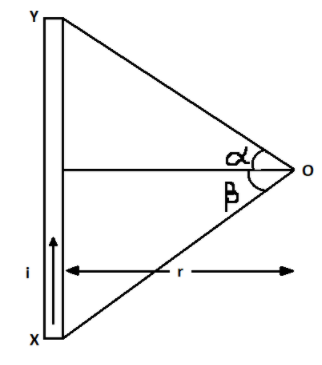
B=4πrμ0i(sinα+sinβ)
Here, μ0 is the permeability of free space
i is the current flowing in the wire
r is the distance of the point to the wire, at which the magnetic field is calculated
α and β are the angles formed with that point
Complete step by step solution:
As we know that the segment LP and QM are along the x-axis. Therefore, they formed an angle of 0∘ with the point O.
So, according to the formula of magnetic field due to a straight wire,
BLP=BMQ=0
Now, the magnetic field due to the segment PS
Segment PS is a half wire and parallel to the y-axis,
Therefore, α=90∘ and β=0∘
Putting these values in the formula for the magnetic field due to straight wire,
BPS=4πrμ0i(sin90∘+sin0∘)
We know that, sin90∘=1
sin0∘=0
On putting the values in the above equation, we get
BPS=4πrμ0i⊗ {direction is into the plane}
Now, the magnetic field due to the segment QN
Since, both the segment PS and QN are equal but the direction is opposite. So, the magnitude of the magnetic field due to the segment QN is equal to the magnetic field due to the segment PSbut the direction is also into the plane.
BQN=4πrμ0i⊗ {direction is into the plane}
Now, the magnetic field at point O is given by,
BO=BPS+BQN+BLP+BMQ
On putting all the values in the above equation , we get
BO=4πrμ0i+4πrμ0i+0+0
As the direction of both BPS and BQN is inward. So, we simply add them
⇒BO=2×4πrμ0i …………..(i)
So, in the question we have given the magnitude of the magnetic field at O,
BO=10−4T
And also given the distance OP=OQ=4cm, which is,
r=4×10−2m
We know that, 4πμ0=10−7NA−2
On putting all the values in equation (i), we get
⇒10−4=4×10−22×10−7×i
On further solving, we get the magnitude of the current,
i=20A
Thus, we get the magnitude of the current is 20A and the direction of the magnetic field at O will be perpendicular to the page.
Therefore, the correct answer is option (D).
Note: The direction of the magnetic field in the wire is found with the right hand thumb rule. If you hold the wire with your right hand so that your thumb points along the current, then your fingers wrap around the wire in the same sense as the magnetic field direction.
